
科目:高中数学 来源: 题型:044
若An,Bn分别表示数列的{an},{bn}前n项的和,对于任意正整数n,an=-n-![]() ,4Bn-12An=13n.
,4Bn-12An=13n.
(1)求数列{bn}的通项公式;
(2)设有抛物线列C1,C2,…,Cn,…,抛物线Cn(n是正整数)的对称轴平衡于y轴,顶点(an,bn),且通过点Dn(0,n2+1),过点Dn且与抛物线相切的直线斜率为kn,求极限![]() .
.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1)求数列{bn}的通项公式;
(2)设有抛物线列C1,C2,…,Cn,…,抛物线Cn(n是正整数)的对称轴平衡于y轴,顶点(an,bn),且通过点Dn(0,n2+1),过点Dn且与抛物线相切的直线斜率为kn,求极限![]() .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省天门市部分重点中学联考高三(上)期中数学试卷(解析版) 题型:解答题
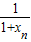 +
+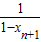 ,数列{an}的前n项和为Tn.求证:Tn>2n-
,数列{an}的前n项和为Tn.求证:Tn>2n- .
.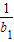 )(1+
)(1+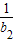 )…(1+
)…(1+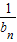 )≥a
)≥a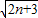 成立,求正数a的取值范围.
成立,求正数a的取值范围.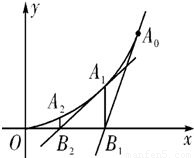
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省六安市霍邱一中高三第二次质量检测数学试卷(理科)(解析版) 题型:解答题
 +
+ ,数列{an}的前n项和为Tn.求证:Tn>2n-
,数列{an}的前n项和为Tn.求证:Tn>2n- .
. )(1+
)(1+ )…(1+
)…(1+ )≥a
)≥a 成立,求正数a的取值范围.
成立,求正数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求数列{bn}的通项公式;
(2)设有抛物线列c1、c2、…cn、…,抛物线cn(n∈N)的对称轴平行于y轴,顶点为(an,bn),且通过点Dn(0,n2+1),过点Dn且与抛物线cn相切的直线斜率为kn,求极限![]() ;
;
(3)设集合X={x|x=2an,n∈N},Y={y|y=4bn,n∈N}.若等差数列{cn}的任一项cn∈X∩Y,
c1是X∩Y中的最大数,且-265<c10<-125,求{cn}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com