解:(Ⅰ)解:(1)当k=2时,f(x)=|x
2-1|+x
2+kx
①当x
2-1≥0时,即x≥1或x≤-1时,方程化为2x
2+2x-1=0
解得

,因为
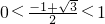
,故舍去,所以

.
②当x
2-1<0时,-1<x<1时,方程化为2x+1=0
解得

由①②得当k=2时,方程f(x)=0的解所以

或

.
(II)解:不妨设0<x
1<x
2<2,
因为
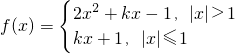
所以f(x)在(0,1]是单调函数,故f(x)=0在(0,1]上至多一个解,
若1<x
1<x
2<2,则x
1x
2=

<0,故不符题意,因此0<x
1≤1<x
2<2.
由f(x
1)=0得

,所以k≤-1;
由f(x
2)=0得

,所以

;
故当

时,方程f(x)=0在(0,2)上有两个解.
当0<x
1≤1<x
2<2时,

,2x
22+kx
2-1=0
消去k得2x
1x
22-x
1-x
2=0
即

,因为x
2<2,所以

.
分析:(1)当k=2时,方程是含有绝对值的方程,对绝对值内的值进行分类讨论去掉绝对值后解之;
(2)先将含有绝对值的函数转化为一元一次函数和二元一次函数的分段函数的形式,再利用一元一次函数与二元
一次函数的单调性加以解决.
点评:本题主要考查的高考考点:函数的基本性质、方程与函数的关系等基础知识;易错点:解析问题的能力较差,分类讨论的问题考虑不全面备考提示:本题还考查函数的基本性质、方程与函数的关系等基础知识,以及综合运用所学知识、分类讨论等思想方法解析和解决问题的能力.需要考生有较扎实的理论知识及较强的解析问题的能力,同时要具备良好的运算能力.

 .
. ,因为
,因为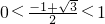 ,故舍去,所以
,故舍去,所以 .
.
 或
或 .
.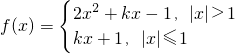
 <0,故不符题意,因此0<x1≤1<x2<2.
<0,故不符题意,因此0<x1≤1<x2<2. ,所以k≤-1;
,所以k≤-1; ,所以
,所以 ;
; 时,方程f(x)=0在(0,2)上有两个解.
时,方程f(x)=0在(0,2)上有两个解. ,2x22+kx2-1=0
,2x22+kx2-1=0 ,因为x2<2,所以
,因为x2<2,所以 .
.
