
已知正三棱柱ABC-A1B1C1所有的棱长都为2,E是A1B的中点,F在棱CC1上.
(1)当C1F=![]() CF时,求多面体ABCF
CF时,求多面体ABCF![]() A1的体积;
A1的体积;
(2)当点F使得A1F+BF为最小时,求异面直线![]() AE与A1F所成的角.
AE与A1F所成的角.
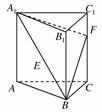
解:(1)∵C1F=![]() CF,AC=CC1=2,
CF,AC=CC1=2,
![]()
由正三棱柱知△ABC的高为![]() 且等于四棱锥B-A1ACF的高.
且等于四棱锥B-A1ACF的高.
![]()
即多面体ABCFA1的体积为![]()
![]() .
.
(2)将侧面BCC1B1展开到侧面A1ACC1得到矩形ABB1A1,连接A1B交C1C于点F,此时点F使得A1F+BF为最小.此时FC平行且等于A1A的一半,
∴F为C1C的中点.
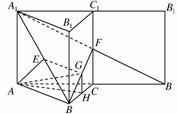
过E作EG∥A1F交BF于G,连接AG,则∠AEG就是AE与A1F所成的角或所成角的补角.
过G作GH⊥BC,交BC于H,连接AH,
则GH=![]() FC=
FC=![]() .又AH=
.又AH=![]() ,于是在Rt△AGH中,
,于是在Rt△AGH中,
AG=![]() =
=![]() ;在Rt△ABA1中,AE=
;在Rt△ABA1中,AE=![]() .
.
∴△AEG中,c![]() os∠AEG=
os∠AEG=![]()
=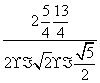 =0,
=0,
∴∠AEG=90°.
故异面直线AE、A1F所成的角为90°.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
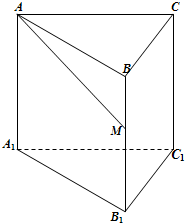 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| AM |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
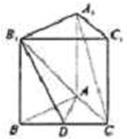 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com