练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    一艘渔船停泊在距岸9km处，今需派人送信给距渔船km处的海岸边渔站，如果送信人步行每小时5km，船速每小时4km，问应在距渔站多少远处登岸再步行可以使抵达渔站的时间最省?

    答案：3km
    解析：

    解：如图所示，设BC为海岸，渔船在点A处，渔站在点C处，∵AB=9，，，设CD=x

    ，，令，解得x=3．∵在x=3附近，由负到正，因此在x=3处取得极小值，又，，．比较可知t(3)最小．故在距渔站3km处登岸可以使抵达渔站的时间最省．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：导学大课堂选修数学1-1苏教版 苏教版 题型：044

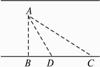
    如图，一艘渔船停泊在距岸9 km的A处，今需派人送信给距渔船km处的海岸渔站C，若送信人步行速度为每小时5 km，船速为每小时4 km，问在何处上岸，可以使抵站的时间最省？[参考导数公式·(x)]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，一艘渔船停泊在距岸9 km的A处，今需派人送信给距渔船3 km处的海岸渔站C，若送信人步行速度为每小时5 km，船速为每小时4 km，问在何处上岸，可以使抵站的时间最省？［参考导数公式（）′=·］

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如右图,一艘渔船停泊在距岸9 km的A处,今需派人送信给距渔船3 km处的海岸渔站C,若送信人步行速度为每小时5 km,船速为每小时4 km,问在何处上岸,可以使抵站的时间最省?〔参考导数公式()′=·f′(x)〕

    查看答案和解析>>

    同步练习册答案