练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    数f(x)＝2(m＋1)x2＋4mx＋2m－1的一个零点在原点，则m的值是________

    答案：
    解析：

    　　答案：

    　　解析：由题意得f(0)＝0，即2m－1＝0，解得m＝．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2004年高考教材全程总复习试卷·数学 题型：044

    已知偶函数y＝f(x)＝ax2＋bx＋c的最小值为－1，且f(1)＝0．

    (1)求该函数的表达式f(x)．

    (2)过曲线C：y＝f(x)(x＞0)上的点P作曲线C的切线，与x轴、y轴分别交于点M，N，试确定点P的坐标，使△MON的面积最小．

    [求商的导数的法则是：＝]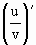

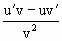    查看答案和解析>>

    科目：高中数学 来源：安徽省淮南市二中2012届高三第三次月考数学理科试题 题型：044

    已知函数f(x)＝alnx－bx2图象上一点P(2，f(2))处的切线方程为y＝－3x＋2ln2＋2．

    (1)求a，b的值；

    (2)若方程f(x)＝m＝0在[，e]内有两个不等实根，求m的取值范围(e为自然对数的底数)；

    (3)令g(x)＝f(x)－kx，若g(x)的图象与x轴交于A(x1，0)，B(x2，0)(其中x1＜x2)，AB的中点为C(x0，0)，求证：g(x)在x0处的导数≠0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设M是满足下列条件的函数f(x)构成的集合：“①方程f(x)－x＝0有实数根；②函数f(x)的导数f′(x)满足0<f′(x)<1.”

    (1)若函数f(x)为集合M中的任一元素，试证明方程f(x)－x＝0只有一个实根；

    (2)判断函数g(x)＝－＋3(x>1)是否是集合M中的元素，并说明理由；

    (3)“对于(2)中函数g(x)定义域内的任一区间[m，n]，都存在x0∈[m，n]，使得g(n)－g(m)＝(n－m)g′(x0)”，请利用函数y＝lnx的图像说明这一结论．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河北省高三8月月考理科数学试卷（解析版） 题型：解答题

    已知函数f(x)＝ax3＋bx2＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3.

    (1)求f(x)的解析式；

    (2)若过点A(2，m)可作曲线y＝f(x)的三条切线，求实数m的取值范围．

    【解析】本试题主要考查了导数在研究函数中的运用。第一问，利用函数f(x)＝ax3＋bx2＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3，得到c＝－3　∴a＝1, f(x)＝x3－3x

    (2)中设切点为(x0，x03－3x0)，因为过点A(2，m)，所以∴m－(x03－3x0)＝(3x02－3)(2－x0)分离参数∴m＝－2x03＋6x02－6

    然后利用g(x)＝－2x3＋6x2－6函数求导数，判定单调性，从而得到要是有三解，则需要满足－6<m<2

    解：(1)f′(x)＝3ax2＋2bx＋c

    依题意

    又f′(0)＝－3

    ∴c＝－3　∴a＝1　∴f(x)＝x3－3x

    (2)设切点为(x0，x03－3x0)，

    ∵f′(x)＝3x2－3，∴f′(x0)＝3x02－3

    ∴切线方程为y－(x03－3x0)＝(3x02－3)(x－x0)

    又切线过点A(2，m)

    ∴m－(x03－3x0)＝(3x02－3)(2－x0)

    ∴m＝－2x03＋6x02－6

    令g(x)＝－2x3＋6x2－6

    则g′(x)＝－6x2＋12x＝－6x(x－2)

    由g′(x)＝0得x＝0或x＝2

    ∴g(x)在(－∞，0)单调递减，(0,2)单调递增，(2，＋∞)单调递减．

    ∴g(x)极小值＝g(0)＝－6，g(x)极大值＝g(2)＝2

    画出草图知，当－6<m<2时，m＝－2x3＋6x2－6有三解，

    所以m的取值范围是(－6,2)．

     

    查看答案和解析>>

    同步练习册答案