练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    奇函数y=f(x)图象在［m,n］(m＞0)上是连续不断的,且f(m)·f(n)＜0,求证:函数y=f(x)在(-n,-m)内有零点.

    证明：由条件得存在c∈［m,n］，且f(c)=0，

        ∵y=f(x)是奇函数，

        ∴f(-c)=-f(c)=0.

        ∵m＜c＜n,

        ∴-n＜-c＜-m,∴y=f(x)在（-n,-m）内有零点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    16．(2)解（1）当a=1,b=-2时，g(x)=f(x)-2,把f(x)图象向下平移两个单位就可得到g(x)图象，

    这时函数g(x)只有两个零点，所以（1）不对

    （2）若a=-1,-2<b<0,则把函数f(x)作关于x轴对称图象，然后向下平移不超过2个单位就可得到g(x)图象，这时g(x)有超过2的零点

    （3）当a<0时， y=af(x)根据定义可断定是奇函数，如果b≠0，把奇函数y=af(x)图象再向上（或向下）平移后才是y=g(x)=af(x)+b的图象，那么肯定不会再关于原点对称了，肯定不是奇函数；当b=0时才是奇函数，所以(3)不对。所以正确的只有(2)

    为了考察高中生学习语文与数学之间的关系，在某中学学生中随机地抽取了610名学生得到如下列表：

    　语文

    数学

    及格

    不及格

    总计　

    及格

    310

    142

    452

    不及格

    94

    64

    158

    总计

    404

    206

    610

     由表中数据计算及的观测值问在多大程度上可以认为高中生的语文与数学成绩之间有关系？为什么？

    查看答案和解析>>

    科目：高中数学 来源：2012届云南省建水一中高三11月月考理科数学 题型：单选题

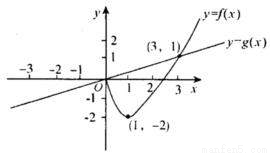
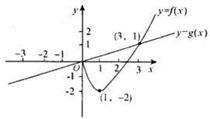
    对任意的实数a、b ，记．若，其中奇函数y=f(x)在x=l时有极小值-2，y=g(x)是正比例函数，函数与函数y=g(x)的图象如图所示．则下列关于函数的说法中，正确的是(   )

    A．为奇函数B．的最小值为-2且最大值为2
    C．在上为增函数D．有极大值且有极小值

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年山东省高三上学期第四次月考理科数学 题型：选择题

    对任意的实数a、b记 若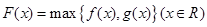，其中

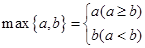
    奇函数y=f(x)在x=l时有极小值-2，y=g(x)是正比例函数，函数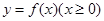与函数y=g(x)的图象如图所示．则下列关于函数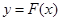的说法中，正确的是 (    )

    A.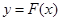为奇函数             B. 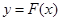的最小值为-2且最大值为2

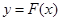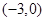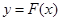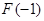    C.在上为增函数    D.有极大值且有极小值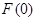

     

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年云南省高三11月月考理科数学 题型：选择题

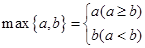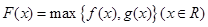    对任意的实数a、b ，记．若，其中奇函数y=f(x)在x=l时有极小值-2，y=g(x)是正比例函数，函数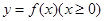与函数y=g(x)的图象如图所示．则下列关于函数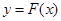的说法中，正确的是(   )

    A.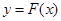为奇函数            B. 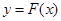的最小值为-2且最大值为2

    C.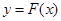在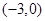上为增函数    D.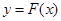有极大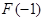值且有极小值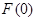

     

    查看答案和解析>>

    同步练习册答案