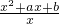练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知g（x）=数学公式，x∈（0，+∞），是否存在实数a，b，使g（x）同时满足下列两个条件：（1）g（x）在（0，1）上是减函数，在[1，+∞）上是增函数；（2）g（x）的最小值是3．若存在，求出a、b，若不存在，说明理由．

    解：∵g（x）=，∴g′（x）=1-
    ∵g（x）在（0，1）上是减函数，在[1，+∞）上是增函数，
    ∴g′（1）=0，∴b=1
    ∵g（x）的最小值是3
    ∴g（1）=1+a+b=3，∴a=1
    综上，a=1，b=1．
    分析：求导函数，利用函数的单调性，可得g′（1）=0，利用g（x）的最小值是3，可得g（1）=0，由此即可得到结论．
    点评：本题考查函数的单调性与最值，考查学生分析解决问题的能力，正确运用函数的单调性与最值是关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    x
    ax-1
    的图象过点（2，2）
    （1）求函数f（x）的解析式；
    （2）设函数g(x)=
    1
    x
    ，则g(x)    的图象经过怎样的变换可与函数f（x）的图象重合；
    （3）设函数h（x）=f（x）•g（x），求h（x）在（1，5]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2011年高三数学第一轮基础知识训练（20）（解析版） 题型：解答题

    已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-kx3．（k≥0）
    （Ⅰ）求g（x）的解析式；
    （Ⅱ）讨论函数f（x）在区间（-∞，0）上的单调性；
    （Ⅲ）若，设g（x）是函数f（x）在区间[0，+∞）上的导函数，问是否存在实数a，满足a＞1并且使g（x）在区间上的值域为，若存在，求出a的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数g（x）=数学公式sin（2x+数学公式），f（x）=acos2（x+数学公式）+b，且函数y=f（x）的图象是函数y=g（x）的图象按向量a=（-数学公式，数学公式）平移得到的．
    （1）求实数a、b的值；
    （2）设h（x）=g（x）-数学公式f（x），求h（x）的最小值及相应的x的值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知函数f(x)=
    x
    ax-1
    的图象过点（2，2）
    （1）求函数f（x）的解析式；
    （2）设函数g(x)=
    1
    x
    ，则g(x)    的图象经过怎样的变换可与函数f（x）的图象重合；
    （3）设函数h（x）=f（x）•g（x），求h（x）在（1，5]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年山东省德州市乐陵一中高三（上）期末数学复习训练试卷22（解析版） 题型：解答题

    已知函数g（x）=sin（2x+），f（x）=acos2（x+）+b，且函数y=f（x）的图象是函数y=g（x）的图象按向量a=（-，）平移得到的．
    （1）求实数a、b的值；
    （2）设h（x）=g（x）-f（x），求h（x）的最小值及相应的x的值．

    查看答案和解析>>

    同步练习册答案