科目：高中数学 来源： 题型：
已知函数f(x)的定义域为R，且对m、n∈R,恒有f(m+n)=f(m)+f(n)－1,且f(－
)=0,当x>－时，f(x)>0.
(1)求证:f(x)是单调递增函数；
(2)试举出具有这种性质的一个函数，并加以验证.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年江苏苏州市高三调研测试文科数学试卷（解析版） 题型：解答题
已知a，b为常数，a?0，函数
．
（1）若a=2，b=1，求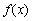
在（0，∞）内的极值；
（2）①若a>0，b>0，求证：
在区间[1，2]上是增函数；
②若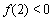
，
，且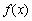
在区间[1，2]上是增函数，求由所有点
形成的平面区域的面积．
查看答案和解析>>
科目：高中数学 来源：2014届甘肃省武威市高二下学期期中测试文科数学试卷（解析版） 题型：选择题
已知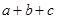
>0,
>0,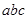
>0,用反证法求证
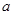>0,
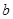>0,c>0的假设为
A．
不全是正数 B．a<0,b<0,c<0 C．a≤0,b>0,c>0 D．abc<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
>0，求证
．
，
>0，故只要证
， 
．
，
，即
，亦即
>
.