练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，平面ADB∩平面BCD=BD，直线EH平面BCD且直线EH∩直线FG=P．

    求证：则点P在直线BD上．
    答案：略
    解析：

    证明：∵PÎ EH，EH平面ABD，

    ∴PÎ 平面ABD．

    又∴PÎ FG，FG平面BCD，

    ∴PÎ 平面BCD．

    ∴点P是平面ABD与平面BCD的公共点．

    ∵平面ABD∩平面BCD=BD，

    ∴PÎ BD．

    　　直线BD是两个平面的公共线，根据公理3可证．

    　　证明点共线问题一般转化为点是某两个平面的公共点，这样根据公理3证明这些点都在这两个平面的交线上．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，A，B，C，D为空间四点．在△ABC中，AB=2，AC=BC=
    		2
    ．
    等边三角形ADB以AB为轴运动．
    （Ⅰ）当平面ADB⊥平面ABC时，求CD；
    （Ⅱ）当△ADB转动时，是否总有AB⊥CD？证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

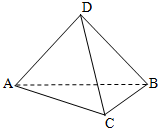    精英家教网如图，A、B、C、D是空间四点，在△ABC中，AB=2，AC=BC=
    		2
    ，等边△ADB所在的平面以AB为轴可转动．
    （Ⅰ）当平面ADB⊥平面ABC时，求三棱锥D-ABC的体积；
    （Ⅱ）当△ADB转动过程中，是否总有AB⊥CD？请证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学空间图形的平行关系、垂直关系专项训练（河北） 题型：解答题

    如右图，A、B、C、D为空间四点．在△ABC中，AB＝2，AC＝BC＝.等边三角形ADB以AB为轴运动．

    (1)当平面ADB⊥平面ABC时，求CD；

    (2)当△ADB转动时，是否总有AB⊥CD?

    证明你的结论．

     

    查看答案和解析>>

    科目：高中数学 来源：2014届山东省高一12月月考数学试卷 题型：解答题

    如图，A、B、C、D是空间四点，在△ABC中，AB=2，AC=BC=，等边△ADB所在的平面以AB为轴可转动.

    （Ⅰ）当平面ADB⊥平面ABC时，求三棱锥的体积；

    （Ⅱ）当△ADB转动过程中，是否总有AB⊥CD？请证明你的结论

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年山东省潍坊市三县市高一（上）期末数学试卷（解析版） 题型：解答题

    如图，A、B、C、D是空间四点，在△ABC中，AB=2，AC=BC=，等边△ADB所在的平面以AB为轴可转动．
    （Ⅰ）当平面ADB⊥平面ABC时，求三棱锥D-ABC的体积；
    （Ⅱ）当△ADB转动过程中，是否总有AB⊥CD？请证明你的结论．

    查看答案和解析>>

    同步练习册答案