
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 求出抛物线的焦点坐标,准线方程,然后求出抛物线的准线与双曲线的交点坐标,利用三角形是等边三角形得到p的方程,求出p即可.
解答 解:抛物线的焦点坐标为(0,$\frac{p}{2}$),
准线方程为:y=-$\frac{p}{2}$,
准线方程与双曲线联立可得:$\frac{{x}^{2}}{3}$-$\frac{{p}^{2}}{12}$=1,
解得x=±$\sqrt{3+\frac{{p}^{2}}{4}}$,
因为△ABF为等边三角形,
所以$\frac{\sqrt{3}}{2}$|AB|=p,
即有$\frac{\sqrt{3}}{2}$•2$\sqrt{3+\frac{{p}^{2}}{4}}$=p,
解得p=6.
故选:C.
点评 本题考查抛物线的简单性质,双曲线方程的应用,考查分析问题解决问题的能力以及计算能力,属于中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 2017×2016 | B. | 2016 | C. | 2017 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
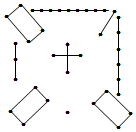 洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.
洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 无意愿 | 有意愿 | 总计 | |
| 男 | a | b | 40 |
| 女 | 5 | d | A |
| 总计 | 25 | B | 80 |
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com