
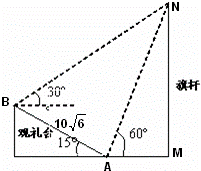
2010年11月12日广州亚运会上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和30°,且座位A、B的距离为![]() 米,则旗杆的高度为 米.
米,则旗杆的高度为 米.
考点:
解三角形的实际应用.
专题:
计算题.
分析:
先画出示意图,根据题意可求得∠NBA和∠BAN,则∠BNA可求,然后利用正弦定理求得AN,最后在Rt△AMN中利用MN=AN•sin∠NAM求得答案.
解答:
解:如图所示,依题意可知∠NBA=45°,
∠BAN=180°﹣60°﹣15°=105°
∴∠BNA=180°﹣45°﹣105°=30°
由正弦定理可知 CEsin∠EAC=ACsin∠CEA,![]()
∴AN=![]() =20
=20![]() 米
米
∴在Rt△AMN中,
MN=AN•sin∠NAM=20![]() ×
×![]() =30米
=30米
所以:旗杆的高度为30米
故答案为:30.
点评:
本题主要考查了解三角形的实际应用.此类问题的解决关键是建立数学模型,把实际问题转化成数学问题,利用所学知识解决.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
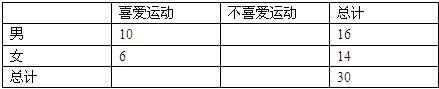
| n(ad-bc)2 | (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 合计 | 30 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
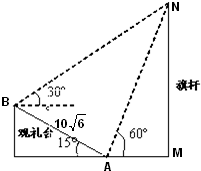 2010年11月12日广州亚运会上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和30°,且座位A、B的距离为10
2010年11月12日广州亚运会上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和30°,且座位A、B的距离为10| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com