
设函数f(x)=xn+bx+c(n∈N+,b,c∈R).
(1)设n≥2,b=1,c=-1,证明:f(x)在区间(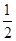 ,1)内存在唯一零点;
,1)内存在唯一零点;
(2)设n为偶数,|f(-1)|≤1,|f(1)|≤1,求b+3c的最小值和最大值;
(3)设n=2,若对任意x1,x2∈[-1,1],有|f(x1)-f(x2)|≤4,求b的取值范围.
(1)见解析 (2)最小值为-6,最大值为0. (3)-2≤b≤2
【解析】
解:(1)当b=1,c=-1,n≥2时,f(x)=xn+x-1,
∵f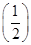 f(1)=
f(1)=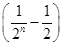 ×1<0,
×1<0,
∴f(x)在(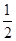 ,1)内存在零点.
,1)内存在零点.
又∵当x∈(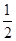 ,1)时,f′(x)=nxn-1+1>0,
,1)时,f′(x)=nxn-1+1>0,
∴f(x)在区间(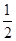 ,1)内单调递增,
,1)内单调递增,
∴f(x)在(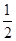 ,1)内存在唯一的零点.
,1)内存在唯一的零点.
(2)依题意知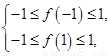
∴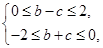 .
.
画出可行域可知b+3c在点(0,-2)处取得最小值-6.在点(0,0)处取得最大值0,因而b+3c的最小值为-6,最大值为0.
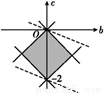
(3)当n=2时,f(x)=x2+bx+c,
对任意x1,x2∈[-1,1]都有|f(x1)-f(x2)|≤4等价于f(x)在[-1,1]上的最大值与最小值之差M≤4,据此分类讨论如下:
若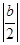 >1,即|b|>2时,
>1,即|b|>2时,
M=|f(1)-f(-1)|=2|b|>4与题设矛盾.
若-1≤-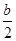 <0,即0<b≤2时,
<0,即0<b≤2时,
M=f(1)-f(-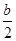 )=(
)=(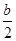 +1)2≤4恒成立.
+1)2≤4恒成立.
若0≤-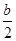 ≤1,即-2≤b≤0时,
≤1,即-2≤b≤0时,
M=f(-1)-f(-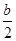 )=(
)=(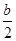 -1)2≤4恒成立.
-1)2≤4恒成立.
综上可知,-2≤b≤2.


科目:高中数学 来源: 题型:
| x |
| a(x+2) |
| 2 |
| 2013 |
| 4 |
| xn |
| ||||
| 2an+1an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com