
如图,C是以AB为直径的半圆O上的一点,过C的直线交直线AB于E,交过A点的切线于D,BC∥OD.
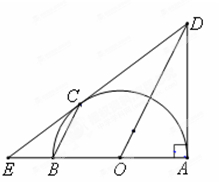
(Ⅰ)求证:DE是圆O的切线;
(Ⅱ)如果AD=AB=2,求EB.
(Ⅰ)见解析;(Ⅱ)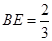 .
.
【解析】
试题分析:(Ⅰ)连接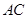 ,
,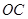 ,根据直径所对的圆心角是直角可知,
,根据直径所对的圆心角是直角可知,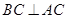 ,结合已知条件“
,结合已知条件“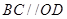 ”得,
”得,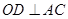 ,所以
,所以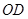 是
是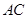 的中垂线,由中垂线的性质可得到,
的中垂线,由中垂线的性质可得到,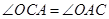 ,
,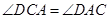 ,把角
,把角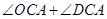 转化为
转化为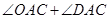 ,即可得到
,即可得到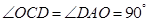 ,则结论可证;(Ⅱ)先根据两个对应角相等得到
,则结论可证;(Ⅱ)先根据两个对应角相等得到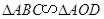 ,由相似三角形对应线段成比例求出线段
,由相似三角形对应线段成比例求出线段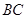 的值,进一步求出
的值,进一步求出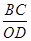 的值,由平行线分线段成比例可得到
的值,由平行线分线段成比例可得到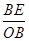 的值,从而解出
的值,从而解出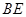 .
.
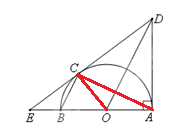
试题解析:(Ⅰ)连接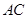 ,
,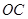 ,
,
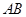 是直径,则
是直径,则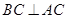 .
.
由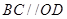 得,
得,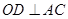 ,
,
则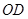 是
是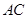 的中垂线,
的中垂线,
所以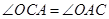 ,
,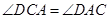 ,
,
所以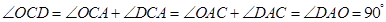 ,
,
则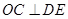 ,即
,即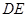 是圆
是圆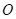 的切线.
5分
的切线.
5分
(Ⅱ)因为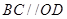 ,
,
所以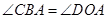 ,
,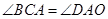 ,
,
则有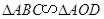 ,
,
所以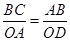 ,那么
,那么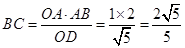 ,
,
所以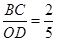 ,
,
所以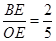 ,
,
所以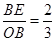 ,
,
解得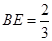 .
10分
.
10分
考点:1.三角形相似的判定及其性质;2.平行线分线段成比例;3.切线的性质及判定


科目:高中数学 来源: 题型:
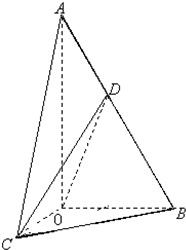 如图,在Rt△AOB中,∠OAB=30°,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在斜边AB上.
如图,在Rt△AOB中,∠OAB=30°,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在斜边AB上.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=| π | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=| π | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
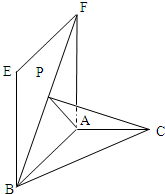 (2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2
(2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2| 3 |
查看答案和解析>>
科目:高中数学 来源:2007-2008学年湖北省宜昌一中、枝江一中、当阳一中三校联合体高三2月联考数学试卷(文科)(解析版) 题型:解答题
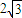 ,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一个动点.
,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一个动点.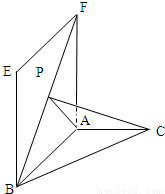
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com