
| π |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 11 |
| 2 |
| 11 |
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a1 |
| 1 |
| a2 |
| 2 |
| a3 |
| 3 |
| a4 |
| 4 |
| 4 |
 |
| i=1 |
| 2S |
| k |
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S4 |
| 4 |
| 4 |
 |
| i=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•上饶二模)如图,设三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,三个侧面与底面所成的二面角O-AB-C,O-BC-A,O-CA-B分别等于α1,α2,α3.记△OAB,△OBC,△OCA,△ABC的面积分别为S1,S2,S3,S,则下列四个命题:(1)Si=Scosαi(i=1,2,3)(2)若∠BAO=∠CAO=45°,则∠BAC=60°(3)S2=S12+S22+S32.(4)α1,α2,α3的取值可以分别是30°,45°,60°.
(2010•上饶二模)如图,设三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,三个侧面与底面所成的二面角O-AB-C,O-BC-A,O-CA-B分别等于α1,α2,α3.记△OAB,△OBC,△OCA,△ABC的面积分别为S1,S2,S3,S,则下列四个命题:(1)Si=Scosαi(i=1,2,3)(2)若∠BAO=∠CAO=45°,则∠BAC=60°(3)S2=S12+S22+S32.(4)α1,α2,α3的取值可以分别是30°,45°,60°.查看答案和解析>>
科目:高中数学 来源: 题型:
 过圆C:(x-1)2+(y-1)2=1的圆心,作直线分别交x,y正半轴于点A、B,△AOB被圆分成I、II、III、IV四个部分(如图),若这四部分图形面积满足①SI+SIV=SII+SIII,②SI+SII+SIII=SIV,则分别满足①、②的直线AB各有( )
过圆C:(x-1)2+(y-1)2=1的圆心,作直线分别交x,y正半轴于点A、B,△AOB被圆分成I、II、III、IV四个部分(如图),若这四部分图形面积满足①SI+SIV=SII+SIII,②SI+SII+SIII=SIV,则分别满足①、②的直线AB各有( )查看答案和解析>>
科目:高中数学 来源: 题型:单选题
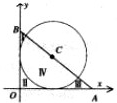 过圆C:(x-1)2+(y-1)2=1的圆心,作直线分别交x,y正半轴于点A、B,△AOB被圆分成I、II、III、IV四个部分(如图),若这四部分图形面积满足①SI+SIV=SII+SIII,②SI+SII+SIII=SIV,则分别满足①、②的直线AB各有
过圆C:(x-1)2+(y-1)2=1的圆心,作直线分别交x,y正半轴于点A、B,△AOB被圆分成I、II、III、IV四个部分(如图),若这四部分图形面积满足①SI+SIV=SII+SIII,②SI+SII+SIII=SIV,则分别满足①、②的直线AB各有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com