
(1)函数f(x)=ax+b(a<0,a、b为常数)在R上是减函数;?
(2)函数g(x)=![]() (k<0,k为常数)在(-∞,0)上是增函数.?
(k<0,k为常数)在(-∞,0)上是增函数.?
证明:(1)设任意的x1、x2∈R,且x1<x2,?
则f(x1)-f(x2)=(ax1+b)-(ax2+b)=a(x1-x2),?
由x1<x2及a<0,得a(x1-x2)>0.?
∴f(x1)-f(x2)>0,即f(x1)>f(x2).?
∴f(x)=ax+b(a<0)在R上为减函数.?
(2)设x1、x2∈(-∞,0),且x1<x2,则g(x1)-g(x2)=![]() -
-![]() =
=![]() ,?
,?
∵x1<x2<0,∴x1x2>0,x2-x1>0.?
又k<0,∴g(x1)-g(x2)<0,即g(x1)<g(x2).?
∴g(x)=![]() (k<0)在(-∞,0)上为增函数.?
(k<0)在(-∞,0)上为增函数.?
点评:证明或判断函数的单调性,严格地说必须用增、减函数定义,其步骤是:设出指定区间上的任意两个值→作差→变形→判符号→定结论.对于正、反比例函数,一、二次函数的单调性,要熟练掌握证明方法,并能结合图象快速指出单调区间.


科目:高中数学 来源:2012-2013学年福建省三明九中高一(上)期中数学试卷(普通班)(解析版) 题型:解答题
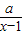 且此函数图象过点(2,1)
且此函数图象过点(2,1)查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高一上学期期中考试数学试题(解析版) 题型:解答题
(12分)函数 是定义域在(-1,1)上奇函数,且
是定义域在(-1,1)上奇函数,且 .
.
(1)确定函数 的解析式;
的解析式;
(2)用定义证明 在(-1,1)上是增函数;
在(-1,1)上是增函数;
(3)解不等式 .
.
查看答案和解析>>
科目:高中数学 来源:2010年河南省辉县市高一上学期第二次阶段性考试数学卷 题型:解答题
(本小题满分12分)
函数 是定义域在(-1,1)上的奇函数,且
是定义域在(-1,1)上的奇函数,且 .
.
(1)确定函数 的解析式;
的解析式;
(2)用定义证明 在(-1,1)上是增函数;
在(-1,1)上是增函数;
(3)解不等式 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com