【答案】
分析:(1)先将式子展开化简,再由幂函数的导数求解即可.
(2)由两个函数商的求导法则,结合对数函数的导数纠结即可.
(3)将tanx转化为正弦和余弦商的形式,由两个函数商的求导法则求解.
(4)首先将函数看作两个函数y=x和y=e
1-cosx的乘积形式,利用两个函数积的求导法则求解,
而y=e
1-cosx为复合函数,求导时应用复合函数求导法则.
解答:解:(1)∵y=(1-
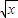
)(1+
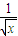
)=
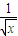
-
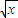
=
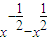
,
∴y′=(x-

)′-(x

)′=-

x-

-

x-

.
(2)y′=(
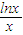
)′=
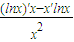
=
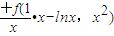
=
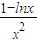
.
(3)y′=(
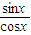
)′=
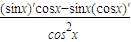
=
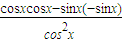
=
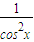
.
(4)y′=(xe
1-cosx)′=e
1-cosx+x(e
1-cosx)′
=e
1-cosx+x[e
1-cosx•(1-cosx)′]
=e
1-cosx+xe
1-cosx•sinx
=(1+xsinx)e
1-cosx.
点评:本题考查导数的求解、导数的运算法则、复合函数的导数,考查运算能力.

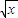 )(1+
)(1+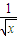 );
);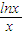 ;
;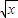 )(1+
)(1+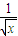 )=
)=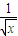 -
-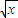 =
=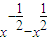 ,
, )′-(x
)′-(x )′=-
)′=- x-
x- -
- x-
x- .
.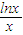 )′=
)′=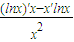 =
=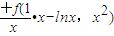 =
=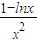 .
.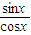 )′=
)′=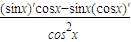
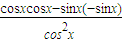 =
=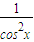 .
.
