
科目:高中数学 来源: 题型:
已知![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() ,
,![]() .
.
⑴设数列![]() 中,
中,![]() ,求证:
,求证:![]() 是等比数列;
是等比数列;
⑵设数列![]() 中,
中,![]() ,求证:
,求证:![]() 是等差数列;
是等差数列;
⑶求数列![]() 的通项公式及前
的通项公式及前![]() 项和.
项和.
【解题思路】由于![]() 和
和![]() 中的项与
中的项与![]() 中的项有关,且
中的项有关,且![]() ,可利用
,可利用![]() 、
、![]() 的关系作为切入点.
的关系作为切入点.
查看答案和解析>>
科目:高中数学 来源:2010-2011年吉林省长春市十一中高一第二学期期中考试理科数学 题型:解答题
.若果数列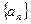 的项构成的新数列
的项构成的新数列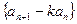 是公比为
是公比为 的等比数
的等比数 列,则相应的数列
列,则相应的数列 是公比为
是公比为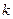 的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列
的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列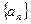 中,
中,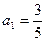 ,
, ,且
,且 .
.
(1)试利用双等比数列法求数列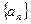 的通项公式;
的通项公式;
(2)求数列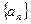 的前
的前 项和
项和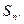
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省高三11月月考文科数学试卷 题型:填空题
记等差数列 的前
的前 项的和为
项的和为 , 利用倒序求和的方法得:
, 利用倒序求和的方法得: ;类似地,记等比数列
;类似地,记等比数列 的前
的前 项的积为
项的积为 ,且
,且
 ),试类比等差数列求和的方法,可将
),试类比等差数列求和的方法,可将 表示成首项
表示成首项 ,末项
,末项 与项数
与项数 的一个关系式,即
的一个关系式,即 =_____________.
=_____________.
查看答案和解析>>
科目:高中数学 来源:2012届北京师大附中高二下学期期中考试理科数学 题型:填空题
记等差数列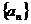 的前
的前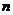 项和
项和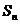 ,利用倒序求和的方法得:
,利用倒序求和的方法得: ;类似的,记等比数列
;类似的,记等比数列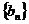 的前
的前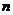 项的积为
项的积为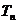 ,且
,且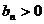
 ,试类比等差数列求和的方法,可将
,试类比等差数列求和的方法,可将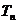 表示成首项
表示成首项 ,末项
,末项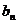 与项数
与项数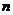 的一个关系式,即公式
的一个关系式,即公式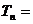 _______________。
_______________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com