
设函数![]() .
.
(1)用定义证明函数![]() 在
在![]() 上为减函数.
上为减函数.
(2)判断函数![]() 的奇偶性.
的奇偶性.
科目:高中数学 来源: 题型:
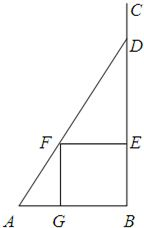 如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2比
如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2比| S1 |
| S2 |
| π |
| 4 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1952 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年黄冈市质检文)(12分) 某公司用480万元购得某种产品的生产技术后,再次投入资金1520万元购买生产设备,进行该产品的生产加工.已知生产这种产品每件还需成本费40元,经过市场调研发现:该产品的销售单价定在100元到300元之间较为合理。当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件产品的销售价格每增加10元,年销售量将减小![]() 万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格每增加10元,年销售量将减小1万件.设销售单价为
万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格每增加10元,年销售量将减小1万件.设销售单价为![]() (元),年销售量为
(元),年销售量为![]() (万件),年获得为
(万件),年获得为![]() (万元).
(万元).
⑴直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
⑵求第一年的年获利![]() 与
与![]() 之间的函数关系式,并说明投资的第一年,该公司是赢利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?
之间的函数关系式,并说明投资的第一年,该公司是赢利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?
查看答案和解析>>
科目:高中数学 来源:2010年河北省2010-2011学年高三第一次月考数学卷 题型:解答题
(本小题满分12分)
某公司用480万元购得某种产品的生产技术后,再次投入资金1520万元购买生产设备,进行该产品的生产加工.已知生产这种产品每件还需成本费40元,经过市场调研发现:该产品的销售单价定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上,每增加10元,年销售量将再减少1万件.设销售单价为 (元),年销售量为
(元),年销售量为 (万件),年获利为
(万件),年获利为 (万元).
(万元).
(1)请写出 与
与 之间的函数关系式;
之间的函数关系式;
(2)求第一年的年获利 与
与 之间的函数关系式,并说明投资的第一年,该公司是赢利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(=1521)
之间的函数关系式,并说明投资的第一年,该公司是赢利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(=1521)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省荆州松滋市高一期末数学试卷(解析版) 题型:解答题
 称为“草花比y”.设∠DAB=θ,正方形BEFG的边长为x.
称为“草花比y”.设∠DAB=θ,正方形BEFG的边长为x. ,求 y的取值范围.
,求 y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com