
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F是A1B1的中点.

(1)求异面直线AE与BF所成的角.
(2)求平面BDF与平面AA1B所成二面角(锐角)的大小.
|
解:如图,建立空间直角坐标系.
∵AB=2,AA1=1,∴A(0,0,0),B(2,0,0),F(1,0,1). 又AD⊥平面ABB1A1,从而BD与平面ABB1A1所成的角为∠DBA=30°. 又AE⊥BD于E,∴AE=1,AD= ∴E( (1)∵ ∴cos〈 ∴异面直线AE、BF所成的角为arccos (2)设平面BDF的一个法向量为n=(x,y,z), 则 令z=1,则n=(1, 又平面ABB1A1的一个法向量为m=(0,1,0). ∴cos〈m,n〉= 即平面BDF与平面AA1B所成二面角(锐角)大小为arccos |
|
求二面角大小时,既可以用先作出平面角,再利用解三角形的知识求解,也可以用向量知识求解.在用向量法求解时,应注意两个问题:一是建系后两个平面的法向量求解正确;二是求出了两法向量夹角后,应结合图形与题意判断求出的是二面角的大小,还是它的补角的大小,从而确定二面角大小. |


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
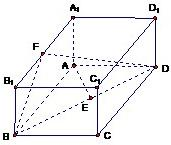 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知长方体ABCD-A1B1C1D1中,AB=2
如图,已知长方体ABCD-A1B1C1D1中,AB=2| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.
如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知长方体ABCD-A′B′C′D′中,AB=2
如图,已知长方体ABCD-A′B′C′D′中,AB=2| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
(2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com