练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （    ）。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：湖南省高考真题 题型：解答题

    已知数列{an}是首项为a且公比q不等于1的等比数列，Sn是其前n项的和，a1，2a7，3a4成等差数列，
    （Ⅰ）证明：12S3，S6，S12-S6成等比数列；
    （Ⅱ）求和Tn=a1+2a4+3a7+…+na3n-2。

    查看答案和解析>>

    科目：高中数学 来源：模拟题 题型：解答题

    已知在数列{an}中，，当n≥2时，3an+1=4an-an-1(n∈N*)，
    (1)证明：{an+1-an}为等比数列；
    (2)求数列{an}的通项；
    (3)若数列{bn}满足bn=n·an，求{bn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：解答题

    已知等差数列{an}的公差d不为0，设Sn=a1+a2q+…+anqn-1，Tn=a1-a2q+…+（-1）n-1anqn-1，q≠0，n∈N*，
    (1)若q=1，a1=1，S3=15，求数列{an}的通项公式；
    (2)若a1=d，且S1，S2，S3成等比数列，求q的值；
    (3)若q≠±1，证明(1-q)S2n-(1+q)T2n=，n∈N*。

    查看答案和解析>>

    科目：高中数学 来源：安徽省模拟题 题型：解答题

    已知数列{an}满足：a1=2t，t2-2an-1t+an-1an=0，n=2，3，4，…（其中t为常数，且t≠0），
    (Ⅰ)求证：数列为等差数列；
    (Ⅱ)求数列{an}的通项公式；
    (Ⅲ)设，求数列{bn}的前n项和Sn。

    查看答案和解析>>

    科目：高中数学 来源：0119 月考题 题型：解答题

    设C1，C2，…，Cn，…是坐标平面上的一列圆，它们的圆心都在x轴的正半轴上，且都与直线y=x相切，对每一个正整数n，圆Cn都与圆Cn+1相互外切，以rn表示Cn的半径，已知{rn}为递增数列。
    （Ⅰ）证明：{rn}为等比数列；
    （Ⅱ）设r1=1，求数列的前n项和。

    查看答案和解析>>

    科目：高中数学 来源：0119 月考题 题型：填空题

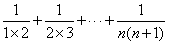    在计算“（n∈N*）”时，某同学学到了如下一种方法：
    先改写第k项：，
    由此得，，…，，
    相加，得，
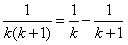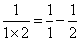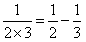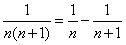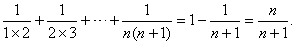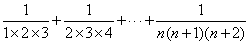    类比上述方法，请你计算“（n∈N*）”，其结果为（    ）。

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：填空题

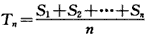    设数列{an}的前n项和为Sn，令，称Tn为数列a1，a2，…，an的“理想数”．已知数列a1，a2，…，a500的“理想数”为2004，那么数列2，a1，a2，…，a500的“理想数”为（    ）。

    查看答案和解析>>

    科目：高中数学 来源：江苏期中题 题型：填空题

    定义“等积数列”为：数列{an}中，对任意n∈N*，都有anan+1=p（常数），则数列{an}称为等积数列，p为公积，现已知数列{an}为等积数列，且a1=1，a2=2，则当n为奇数时，前n项和Sn=（    ）。

    查看答案和解析>>

    同步练习册答案