练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11、如图，点A，B，C确定的平面与点D，E，F确定的平面相交于直线l，且直线AB与l相交于点G，直线EF与l相交于点H，试作出平面ABD与平面CEF的交线．
    分析：欲作出平面ABD与平面CEF的交线，先找两平面的公共点，在平面ABC内，连接AB，与l相交于点G，则G∈平面DEF，在平面DEF内，连接DG，与EF相交于点M，M在平面ABD与平面CEF的公共点，同样方法再找另一公共点，两点确定一直线．
    解答：解：如图，在平面ABC内，连接AB，与l相交于点G，
    则G∈平面DEF；在平面DEF内，连接DG，
    与EF相交于点M，则M∈平面ABD，且M∈平面CEF．
    所以，M在平面ABD与平面CEF的交线上．
    同理，可作出点N，N在平面ABD与平面CEF的交线上．
    连接MN，直线MN即为所求．
    点评：本题主要考查了平面与平面之间的位置关系，考查空间想象能力、运算能力和推理论证能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，有三个生活小区（均可看成点）分别位于A、B、C三点处，AB=AC，A到线段BC的距离AO=40，∠ABO=
    2π
    7
    （参考数据：tan
    2π
    7
    ≈
    2
    		3
    3
    ）．今计划建一个生活垃圾中转站P，为方便运输，P准备建在线段AO（不含端点）上．
    （I）设PO=x（0＜x＜40），试将P到三个小区距离的最远者S表示为x的函数，并求S的最小值；
    （II）设∠PBO=a（0＜α＜
    2π
    7
    ），试将P到三个小区的距离之和y表示为a的函数，并确定当a取何值时，可使y最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•湖南）在平面直角坐标系xOy中，将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”．如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”．某地有三个新建居民区，分别位于平面xOy内三点A（3，20），B（-10，0），C（14，0）处．现计划在x轴上方区域（包含x轴）内的某一点P处修建一个文化中心．
    （I）写出点P到居民区A的“L路径”长度最小值的表达式（不要求证明）；
    （II）若以原点O为圆心，半径为1的圆的内部是保护区，“L路径”不能进入保护区，请确定点P的位置，使其到三个居民区的“L路径”长度之和最小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•宁德模拟）如图（1），在直角梯形 ABCD 中，AB∥CD，∠C=90°，CD=2AB=2，∠D=60°，E为DC中点，将四边形ABCE绕直线AE旋转90°得到四边形AB′C′E，
    如图（2）．
    （I）求证：EA⊥B′B；
    （II）线段B′C′上是否存在点M，使得EM∥平面DB′B，若存在，确定点M的位 置；若不存在，请说明理由；
    （III）求平面CB′D与平面BB′A所成的锐二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

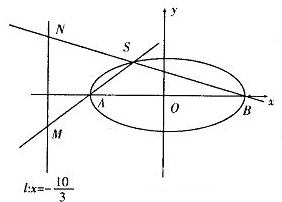    （2013•临沂一模）如图，已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的左、右顶点为A、B，离心率为
    		3
    2
    ，直线x-y+l=0经过椭圆C的上顶点，点S是椭圆C上位于x轴上方的动点，直线AS，BS与直线l：x=-
    10
    3
    分别交于M，N两点．
    （I）求椭圆C的方程；
    （Ⅱ）求线段MN长度的最小值；
    （Ⅲ）当线段MN长度最小时，在椭圆C上是否存在这样的点P，使得△PAS的面积为l？若存在，确定点P的个数；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江苏省南通市通州区高三（下）2月寒假调研数学试卷（解析版） 题型：解答题

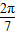    如图，有三个生活小区（均可看成点）分别位于A、B、C三点处，AB=AC，A到线段BC的距离AO=40，∠ABO=（参考数据：tan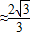）．今计划建一个生活垃圾中转站P，为方便运输，P准备建在线段AO（不含端点）上．
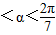    （I）设PO=x（0＜x＜40），试将P到三个小区距离的最远者S表示为x的函数，并求S的最小值；
    （II）设∠PBO=a（0），试将P到三个小区的距离之和y表示为a的函数，并确定当a取何值时，可使y最小？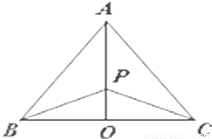

    查看答案和解析>>

    同步练习册答案