
(本题满分12分)如图,在平面直角坐标系xOy中,AB是半圆⊙O:x2 + y2 = 1(y≥0)的直径,C是半圆O(除端点A、B)上的任意一点,在线段AC的延长线上取点P,使︱PC︱=︱BC︱,试求动点P 的轨迹方程.
 |
解 连结BP,由已知得∠APB = 45°. …………………… 2分
设P(x,y),则 ![]() ,
,![]() ,由PA到PB的角为45°,
,由PA到PB的角为45°,
得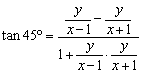 ,化简得 x2 +(y-1)2 = 2. …………………… 10分
,化简得 x2 +(y-1)2 = 2. …………………… 10分
由已知,y>0且![]() >0,故点P的轨迹方程为x2 +(y-1)2 = 2(x>-1,y>0). …………………… 12分
>0,故点P的轨迹方程为x2 +(y-1)2 = 2(x>-1,y>0). …………………… 12分
法二 连结BP,由已知可得∠APB = 45°,∴ 点P在以AB为弦,所对圆周角为45°的圆上.
设该圆的圆心为D,则点D在弦AB的中垂线上,即y轴上,且∠ADB = 90°,∴ D(0,1),︱DA︱=![]() ,圆D的方程为x2 +(y-1)2 = 2.
,圆D的方程为x2 +(y-1)2 = 2.
由已知,当点C趋近于点B时,点P趋近于点B;当点C趋近于点A时,点P趋近于点(-1,2),所以点P的轨迹方程为x2 +(y-1)2 = 2(x>-1,y>0).


科目:高中数学 来源:2014届江西高安中学高二上期末考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)
如图所示的几何体是由以正三角形 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.

(1)当 时,求平面
时,求平面 与平面
与平面 的夹角的余弦值;
的夹角的余弦值;
(2)当 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 ?
?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省八市高三3月联考理科数学试卷(解析版) 题型:解答题
(本题满分12分)如图,在长方体 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.

(Ⅰ)确定 点的位置,使得
点的位置,使得 ;
;
(Ⅱ)当 时,求二面角
时,求二面角 的平
的平
面角余弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广西桂林中学高三7月月考试题理科数学 题型:解答题
(本题满分12分)如图,在四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=2,E是PB的中点,F是AD的中点.

⑴求异面直线PD与AE所成角的大小;
⑵求证:EF⊥平面PBC ;
⑶求二面角F—PC—B的大小..
查看答案和解析>>
科目:高中数学 来源:2011年湖南省招生统一考试文科数学 题型:解答题
(本题满分12分)
如图3,在圆锥 中,已知
中,已知 的直径
的直径 的中点.
的中点.
(I)证明:
(II)求直线和平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2010年海南省高三五校联考数学(文) 题型:解答题
(本题满分12分)
如图,三棱锥S—ABC中,AB⊥BC,D、E分别为AC、BC的中点,SA=SB=SC。
(1)求证:BC⊥平面SDE;
(2)若AB=BC=2,SB=4,求三棱锥S—ABC的体积。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com