(本小题满分12分)
解:(Ⅰ)因为函数f(x)=

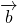
=(cos
2ωx-sin
2ωx,sinωx)•(

,2cosωx)
=

(cos
2ωx-sin
2ωx)+2sinωxcosωx
=

cos2ωx+sin2ωx
=2sin(2ωx+

),
函数f(x)的图象关于直线
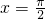
对称,
所以2sin(2ωx+

)=±2,ωπ+

=kπ+

,k∈Z,ω=k+

,k∈Z,
其中ω为常数,且ω∈(0,1).所以ω=

.
函数f(x)=2sin(

x+

);
(Ⅱ)若将y=f(x)图象上各点的横坐标变为原来的

,
再将所得图象向右平移

个单位,纵坐标不变,
得到y=2sin(2x-

)的图象,所以h(x)=2sin(2x-

),
x∈
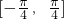
,∴2x-

∈[

],∴2sin(2x-

)∈[-2,1]
h(x)在
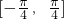
上的取值范围[-2,1].
分析:(Ⅰ)通过向量的数量积以及二倍角公式和两角和的正弦函数,化简函数为 一个角的一个三角函数的形式,通过函数的对称轴方程求出ω,然后得到函数f(x)的表达式;
(Ⅱ)通过函数图象的变换,求出y=h(x),利用x∈
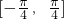
,通过正弦函数的值域,求解函数的取值范围.
点评:本题考查向量的数量积,两角和与差的三角函数,正弦函数的图象与性质,函数图象的平移变换,考查向量与三角函数的综合应用.

 =(cos2ωx-sin2ωx,sinωx),
=(cos2ωx-sin2ωx,sinωx), =(
=( ,2cosωx),函数f(x)=
,2cosωx),函数f(x)=
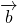 (x∈R)的图象关于直线
(x∈R)的图象关于直线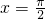 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1). ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)的图象,求y=h(x)在
个单位,纵坐标不变,得到y=h(x)的图象,求y=h(x)在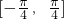 上的取值范围.
上的取值范围.
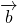 =(cos2ωx-sin2ωx,sinωx)•(
=(cos2ωx-sin2ωx,sinωx)•( ,2cosωx)
,2cosωx) (cos2ωx-sin2ωx)+2sinωxcosωx
(cos2ωx-sin2ωx)+2sinωxcosωx cos2ωx+sin2ωx
cos2ωx+sin2ωx ),
),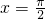 对称,
对称, )=±2,ωπ+
)=±2,ωπ+ =kπ+
=kπ+ ,k∈Z,ω=k+
,k∈Z,ω=k+ ,k∈Z,
,k∈Z, .
. x+
x+ );
); ,
, 个单位,纵坐标不变,
个单位,纵坐标不变, )的图象,所以h(x)=2sin(2x-
)的图象,所以h(x)=2sin(2x- ),
),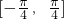 ,∴2x-
,∴2x- ∈[
∈[ ],∴2sin(2x-
],∴2sin(2x- )∈[-2,1]
)∈[-2,1]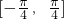 上的取值范围[-2,1].
上的取值范围[-2,1].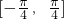 ,通过正弦函数的值域,求解函数的取值范围.
,通过正弦函数的值域,求解函数的取值范围.

 阅读快车系列答案
阅读快车系列答案