

(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PB∥平面AEC;
(Ⅲ)求二面角E-AC-B的大小.
解法一:

(Ⅰ)∵PA⊥平面ABCD,
∴AB是PB在平面ABCD上的射影.
又∵AB⊥AC,AC![]() 平面ABCD,
平面ABCD,
∴AC⊥PB.
(Ⅱ)连接BD,与AC相交于O,连接EO.
∵ABCD是平行四边形,
∴O是BD的中点,
又E是PD的中点,
∴EO∥PB.
又PB![]() 平面AEC,EO
平面AEC,EO![]() 平面AEC,
平面AEC,
∴PB∥平面AEC.
(Ⅲ)过O作FG∥AB,交AD于F,交BC于G,则F为AD的中点.
∵AB⊥AC,
∴OG⊥AC,
又由(Ⅰ),(Ⅱ)知,AC⊥PB,EO∥PB,
∴AC⊥EO.
∴∠EOG是二面角E-AC-B的平面角.
连接EF,在△EFO中,
EF=![]() PA,FO=
PA,FO=![]() AB,又PA=AB,EF⊥PO,
AB,又PA=AB,EF⊥PO,
∴ ∠EOF=45°,∠EOG=135°,
∴二面角E-AC-B的大小为135°.
解法二:
(Ⅰ)建立空间直角坐标系A-xyz,如图.

设AC=a,PA=b,则有A(0,0,0),B(0,b,0),C(a,0,0),P(0,0,b),
∴![]()
∴AC⊥PB.
(Ⅱ)连接BD,与AC相交于O,连接EO.
由已知得D(a,-b,0),
E![]()
∴![]()
又![]()
∴![]()
∴PB∥EO,
又PB![]() 平面AEC,EO
平面AEC,EO![]() 平面AEO,
平面AEO,
∴PB∥平面AEC.
(Ⅲ)取BC中点G,连接OG,则点G的坐标为(![]() ),
),![]()
又![]()
∴![]()
∴OE⊥AC,OG⊥AC,
∴∠EOG是二面角E-AC-B的平面角.
∵cosEOG=cos<![]() ,
,![]() >=
>=
∴∠EOG=135°,
∴二面角E-AC-B的大小为135°.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
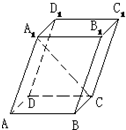 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,若∠A1AB=∠A1AD=60°,且A1A=3,则A1C的长为( )
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,若∠A1AB=∠A1AD=60°,且A1A=3,则A1C的长为( )A、
| ||
B、2
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:

图1-1-17
A.1个 B.2个 C.3个 D.无穷多个
查看答案和解析>>
科目:高中数学 来源: 题型:

(Ⅰ)求证:PB⊥DM;
(Ⅱ) 求CD与平面ADMN所成的角。
查看答案和解析>>
科目:高中数学 来源: 题型:
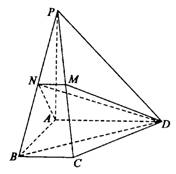
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求BD与平面ADMN所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com