Question

已知数列{a_n},{b_n}满足：a₁=1,a₂=a(a为常数)，且b_n=a_n·a_n+1,其中n=1,2,3…

(1)若{a_n}是等比数列，试求数列{b_n}的前n项和S_n的公式；

(2)当{b_n}是等比数列时，甲同学说：{a_n}一定是等比数列；乙同学说：{a_n}一定不是等比数列，你认为他们的说法是否正确？为什么？

Answer 1

解:(1)∵{a_n}是等比数列a₁=1,a₂=a,?∴a≠0,a_n=a^n-1.

又b_n=a_n·a_n+1则b₁=a₁·a₂=a,===a²，

即{b_n}是以a为首项，a²为公比的等比数列._?

∴S_n=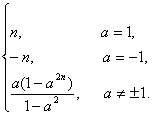

(2)甲、乙两个同学的说法都不正确，理由如下._?

解法1：设{b_n}的公比为q,则===q且a≠0,

又a₁=1,a₂=a,a₁,a₃,a₅,…,a_2n-1,…是以1为首项，q为公比的等比数列，a₂,a₄,a₆,…,a_2n,…是以a为首项，q为公比的等比数列，即{a_n}为：1，a,q,aq,q²,aq²,_?

当q=a²时，{a_n}是等比数列；_?

当q≠a²时，{a_n}不是等比数列._?

解法2：{a_n}可能是等比数列，也可能不是等比数列，举例说明如下：_?

设{b_n}的公比为q_?

①取a=q=1时，a_n=1(n∈N),此时b_n=a_na_n+1=1,{a_n}、{b_n}都是等比数列._?

②取a=2,q=1时，_?

a_n=b_n=2，n∈N.

所以{b_n}是等比数列，而{a_n}不是等比数列.