已知数列{an}的前n项和Sn=12n-n2.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的前n项和Tn.
解:(1)当n=1时,a
1=S
1=12×1-1
2=11;…(1分)
当n≥2时,a
n=S
n-S
n-1=(12n-n
2)-[12(n-1)-(n-1)
2]=13-2n.…(3分)
n=1时,a
1=11也符合13-2n的形式.
所以,数列{a
n}的通项公式为a
n=13-2n.…(4分)
(2)令a
n=13-2n≥0,又n∈N
*,解得n≤6.…(5分)
当n≤6时,T
n=|a
1|+|a
2|+…+|a
n|=a
1+a
2+…+a
n=S
n=12n-n
2;…(8分)
当n>6时,T
n=|a
1|+|a
2|+…+|a
6|+|a
7|+…+|a
n|=a
1+a
2+…+a
6-a
7-a
8-…-a
n=2S
6-S
n=2×(12×6-6
2)-(12n-n
2)
=n
2-12n+72.…(11分)
综上,
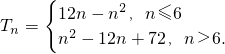
…(12分)
分析:(1)求出a
1,利用n≥2时,a
n=S
n-S
n-1,求出a
n,验证n=1时满足通项公式,即可求得数列{a
n}的通项公式;
(2)利用a
n=13-2n≥0求出整数数列的项数,然后讨论n≤6,n>6时求数列{|a
n|}的前n项和T
n.
点评:本题是中档题,考查数列的通项公式的求法,前n 项和的求法,考查计算能力,注意数列中变符号的项,是常考题型.

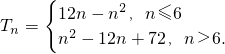 …(12分)
…(12分)

 考前必练系列答案
考前必练系列答案