解:(1)设t=x
2+2x+3,则g(x)=log
4t
∵t=(x+1)2+2≥2,即t∈[2,+∞),
函数g(x)的值域为[

,+∞);
(2)∵f(x)=(x-

)
2+1-

a
2,
当a≥0时,

∈[a,+∞),
这时,y
min=f(

)=1-

a
2;
当a<0时,f(x)在[a,+∞)上是增函数,这时,f(x)在[a,+∞)上的最小值为:
f(a)=1-2a
2综上,函数f(x)在[a,+∞)上的最小值为:
当a≥0时,1-

a
2当a<0时,1-2a
2 (8分)
(3)g(x)在R上的最小值为

由题意得f(x)在[a,+∞)上的最小值大于或等于g(x)在R上的最小值

当a≥0时,由1-

a
2≥

解得
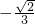
≤a≤

这时,0≤a≤

当a<0时,1-2a
2≥

解得:

≤a≤

这时,

≤a<0
综上,a的取值范围为:

≤a≤

(14分)
分析:(1)要求函数f(x)的值域,只要求t=x
2+2x+3最小值,进而可求函数的值域;
(2)先配方得到函数的对称轴,将对称轴移动,讨论对称轴与区间[a,+∞)的位置关系,合理地进行分类,从而求得函数的最小值;
(3)对于任意x
1∈[a,+∞),总存在x
2∈R,使得f(x
1)≥g(x
2)成立转化为f(x)在[a,+∞)上的最小值大于或等于g(x)在R上的最小值

,列出不等式求出a的范围.
点评:本小题主要考查函数恒成立问题、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.对于二次函数,配方求得函数的对称轴是解题的关键.由于对称轴所含参数不确定,而给定的区间也是不确定的,这就需要分类讨论.利用函数的图象将对称轴移动,合理地进行分类,从而求得函数的最值,当然应注意若求函数的最大值,则需按中间偏左、中间偏右分类讨论.

 .
. ,+∞);
,+∞); )2+1-
)2+1- a2,
a2, ∈[a,+∞),
∈[a,+∞), )=1-
)=1- a2;
a2; a2
a2

 a2≥
a2≥ 解得
解得 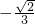 ≤a≤
≤a≤

 解得:
解得: ≤a≤
≤a≤
 ≤a<0
≤a<0 ≤a≤
≤a≤ (14分)
(14分) ,列出不等式求出a的范围.
,列出不等式求出a的范围.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<