【答案】
分析:(I)由几何体的三视图,知该几何体上面是一个长方体,长方体的底面是边长为4的正方形,高是2,求出其表面积;下面是一个正四棱台,上底边长是4的正方形,下底是边长为8的正方形,根据勾股定理做出斜高,得到侧面积,得到正四棱台5个面的面积,最后求和得到结果.
(II)分别求出几何体的上、下两部分的体积后相加即得此几何体的体积.
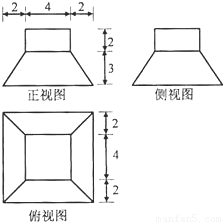
解答:解:(I)由三视图知,几何体是一个组合体,
上面是一个长方体,长方体的底面是边长为4的正方形,高是2,
其表面积S
上=16+4×8=48;
下面是一个正四棱台,上底边长是4的正方形,下底是边长为8的正方形,高是2,
∴斜高是=
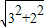
=
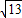
,
∴正四棱台的侧面积是

(4+8)×
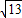
×4=24
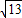
.
下面是一个边长是8的正方形,其面积为64,
∴几何体的表面积是48+24
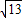
+64=112+24
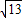
(cm
2);
(II)V=V
1+V
2=4×4×2+

(4
2+8
2+4×8)×3=144cm
3.
点评:本题考查由三视图求几何体的体积和表面积,考查由三视图还原几何图形的直观图,本题是一个基础题,这种题目一般不会进行线面关系的证明,而只是用来求体积和面积.

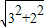 =
=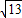 ,
, (4+8)×
(4+8)×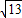 ×4=24
×4=24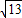 .
.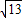 +64=112+24
+64=112+24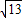 (cm2);
(cm2); (42+82+4×8)×3=144cm3.
(42+82+4×8)×3=144cm3.

