
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
(1)求证:BE∥平面PDA;
(2)若平面PBE与平面ABCD所成的二面角为45°,则线段PD是线段AD的几倍?
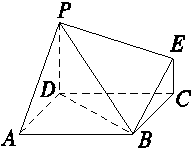
解:(1)证明:∵EC∥PD,PD⊂平面PDA,EC⊄平面PDA
∴EC∥平面PDA,
同理可得BC∥平面PDA.
∵EC⊂平面EBC,BC⊂平面EBC且EC∩BC=C.
∴平面BEC∥平面PDA.
又∵BE⊂平面EBC,
∴BE∥平面PDA.5分
(2)法一:延长PE与DC的延长线交于点G,连结GB,
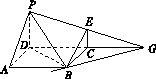
则GB为平面PBE与ABCD的交线.7分
∵PD=2EC,∴CD=CG=CB.
∴D、B、G在以C为圆心、以BC为半径的圆上,
∴DB⊥BG.
∵PD⊥平面ABCD,∴PD⊥BG,且PD∩DB=D,
∴BG⊥面PDB,∴BG⊥PB,
∴∠PBD为平面ABE与平面ABCD所成的二面角的平面角,即∠PBD=45°,10分
∴PD=DB=![]() AD,即
AD,即![]() =
=![]() .
.
∴当平面PBE与平面ABCD所成的二面角为45°时,线段PD是AD的![]() 倍.14分
倍.14分
(2)法二:如图,以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系.设该简单组合体的底面边长为1,设PD=a,则B(1,1,0),C(0,1,0),P(0,0,a),E(0,1,![]() ).
).
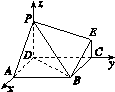
∴=(1,1,-a),=(0,1,-![]() )
)
设n=(x,y,z)为平面PBE的一个法向量,则
.令z=2,得y=a,x=a,即n=(a,a,2).
显然=(0,0,a)为平面ABCD的法向量,9分
∴cos45°==![]() ,解得a=
,解得a=![]() ,即
,即![]() =
=![]() .
.
∴当平面PBE与平面ABCD所成的二面角为45°时,线段PD是AD的![]() 倍.
倍.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.查看答案和解析>>
科目:高中数学 来源: 题型:
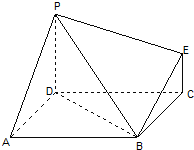 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,| PD |
| AD |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
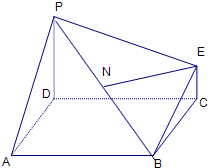 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图为一简单组合体,其底面 ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
如图为一简单组合体,其底面 ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com