练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知数列{an}满足an+1-an=2，a1=-5，则|a1|+|a2|+…+|a6|=（　　）
    A．9B．15C．18D．30

    分析 利用等差数列的通项公式可得an．及其数列{an}的前n项和Sn．令an≥0，解得n，分类讨论即可得出．

    解答 解：∵an+1-an=2，a1=-5，∴数列{an}是公差为2的等差数列．
    ∴an=-5+2（n-1）=2n-7．
    数列{an}的前n项和Sn=$\frac{n（-5+2n-7）}{2}$=n2-6n．
    令an=2n-7≥0，解得$n≥\frac{7}{2}$．
    ∴n≤3时，|an|=-an．
    n≥4时，|an|=an．
    则|a1|+|a2|+…+|a6|=-a1-a2-a3+a4+a5+a6=S6-2S3=62-6×6-2（32-6×3）=18．
    故选：C．

    点评 本题考查了分类讨论方法、等差数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．设定义域为R的函数$f（x）=\left\{{\begin{array}{l}{\frac{4}{{|{x-1}|}}（x≠1）}\\{2（x=1）}\end{array}}\right.$，若关于x的方程f2（x）+bf（x）+c=0有三个不同的实数解x1，x2，x3，则${x_1}^2+{x_2}^2+{x_3}^2$=11．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知四面体ABCD的顶点都在球O表面上，且AB=BC=AC=2$\sqrt{2}$，DA=DB=DC=2，过AD作相互垂直的平面α、β，若平面α、β截球O所得截面分别为圆M、N，则（　　）
    A．MN的长度是定值$\sqrt{2}$B．MN长度的最小值是2
    C．圆M面积的最小值是2πD．圆M、N的面积和是定值8π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知复数z=1+2i，则$\overline z$=（　　）
    A．1-2iB．5+4iC．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．如图，在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥底面ABCD，AD=AP=2，AB=2$\sqrt{7}$，E为棱PD中点．
    （1）求证：PD⊥平面ABE；
    （2）求四棱锥P-ABCD外接球的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

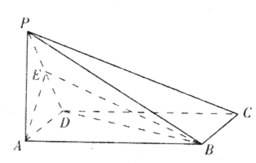    3． 如图，四棱锥P-ABCD的底面ABCD为矩形，PA⊥底面ABCD，AD=AP=2，AB=2$\sqrt{7}$，E为棱PD的中点．
    （Ⅰ）证明：PD⊥平面ABE；
    （Ⅱ）求三棱锥C-PBD外接球的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．若cos（$\frac{π}{8}$-α）=$\frac{1}{6}$，则cos（$\frac{3π}{4}$+2α）的值为（　　）
    A．$\frac{17}{18}$B．-$\frac{17}{18}$C．$\frac{18}{19}$D．-$\frac{18}{19}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

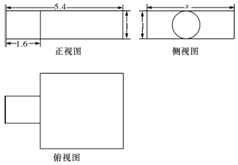    7．中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器----商鞅铜方升，其三视图（单位：寸）如图所示，若π取3，其体积为12.6（立方寸），则图中的x为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．等差数列{an}的前n项和为Sn，且S5=15，a2=5，则公差d等于（　　）
    A．-3B．-2C．-1D．2

    查看答案和解析>>

    同步练习册答案