练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若＝(－2，1)是直线l的一个法向量，则l的倾斜角的大小为________(结果用反三角函数值表示)．

    答案：arctan2
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：高三数学教学与测试 题型：044

    已知直四棱柱ABCD－的底面ABCD是矩形，又＝AB，E，F分别是和AD的中点．(1)求异面直线EF和所成的角；(2)证明EF是异面直线AD和的公垂线；(3)又若G是的中点，求证：平面．

    查看答案和解析>>

    科目：高中数学 来源：甘肃省兰州一中2010届高三上学期期末考试数学(理)试题 题型：044

    如图，在直三棱柱ABC－A1B1C1中，AB⊥BC，AB＝BC＝1，AA1＝2，D是AA1的中点．

    (1)求证：B1C⊥BA；

    (2)求二面角C－B1D－B的大小；

    (3)在B1C上是否存在一点E，使得DE∥平面ABC？若存在，求出的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：广东省实验中学2012届高三下学期综合测试(一)数学理科试题 题型：044

    如图，P－AD－C是直二面角，四边形ABCD是∠BAD＝120°的菱形，AB＝2，PA⊥AD，E是CD的中点，设PC与平面ABCD所成的角为45°．

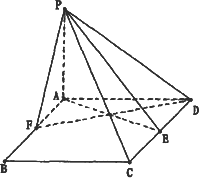
    (1)求证：平面PAE⊥平面PCD；

    (2)试问在线段AB(不包括端点)上是否存在一点F，使得二面角A－PE－D的大小为45°？若存在，请求出AF的长，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分12分）如图，五面体A－BCC1B1中，AB1＝4，底面ABC是正三角形，AB＝2，四边形BCC1B1是矩形，二面角A－BC－C1为直二面角，D为AC中点.

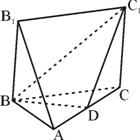    （1）求证：AB1∥面BDC1；（2）求二面角C－BC1－D的大小；

    （3）若A、B、C、C1为某一个球面上四点，求球的半径.

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年河南省卫辉市高三2月月考数学理卷 题型：选择题

    下列命题中不正确命题的个数是（　　）

    ①经过空间一点一定可作一平面与两异面直线都平行；

    ②已知平面、，直线a、b，若，，则；

    ③有两个侧面垂直于底面的四棱柱为直四棱柱；

    ④四个侧面两两全等的四棱柱为直四棱柱；

    ⑤底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；

    ⑥底面是等边三角形，∠APB＝∠BPC＝∠CPA，则三棱锥P－ABC是正三棱锥.

    A．0                               B．1           C．2                             D．3

     

    查看答案和解析>>

    同步练习册答案