
数列﹛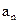 ﹜中,
﹜中,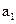 =
=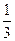 ,前n项和
,前n项和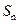 满足
满足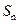 +1-
+1-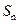 =(
=(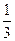 )n+1 (n
)n+1 (n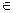 N*
N* )
)
(1)求数列﹛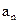 ﹜的通项公式
﹜的通项公式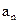 以及前n项和
以及前n项和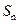
(2)若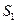 ,t(
,t(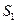 +
+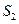 ), 3(
), 3(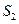 +
+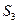 )成等差数列,求实数t的值。
)成等差数列,求实数t的值。
科目:高中数学 来源:2007年高邮市第二中学高三数学模拟试卷 题型:013
在等待数列{an}中,Sn表示前n项和,且a2+a8=18-a5,则S9=
A.18
B.60
C.54
D.27
查看答案和解析>>
科目:高中数学 来源:2009届宁夏省期末数学模拟试题分类汇编(数列) 题型:013
在各项均为正数的数列{an}中,Sn为前n项和,n![]() =(n+1)
=(n+1)![]() +anan+1且a3=π,则tanS4=
+anan+1且a3=π,则tanS4=
A.-![]()
B.![]()
C.-![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源:河北省唐山一中2010届高三仿真模拟卷数学理科试题(一) 题型:013
在各项均为正数的数列{an}中,Sn为前n项和,n![]() =(n+1)
=(n+1)![]() +anan+1且a3=π,则tanS4=
+anan+1且a3=π,则tanS4=
-![]()
![]()
-![]()
![]()
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试、文科数学(福建卷) 题型:044
数列{an}中a=![]() ,前n项和Sn满足Sn+1-Sn=
,前n项和Sn满足Sn+1-Sn=![]() (n∈N*).
(n∈N*).
(Ⅰ)求数列{an}的通项公式an以及前n项和Sn;
(Ⅱ)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值.
查看答案和解析>>
科目:高中数学 来源:甘肃省兰州一中2012届高三上学期期中考试数学文科试题 题型:044
已知数列{an}中a1=2,an+1=2-![]() ,数列{bn}中bn=
,数列{bn}中bn=![]() ,其中n∈N*.
,其中n∈N*.
(Ⅰ)求证:数列{bn}是等差数列;
(Ⅱ)设Sn是数列{![]() }的前n项和,求
}的前n项和,求![]() ;
;
(Ⅲ)设Tn是数列![]() 的前n项和,求证:
的前n项和,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com