
已知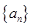 为等差数列,
为等差数列,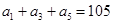 ,
,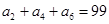 ,
,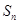 是等差数列
是等差数列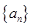 的前
的前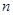 项和,则使得
项和,则使得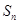 达到最大值的
达到最大值的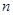 是
是
| A.21 | B.20 | C.19 | D.18 |
B
解析考点:等差数列的前n项和.
专题:计算题.
分析:写出前n项和的函数解析式,再求此式的最值是最直观的思路,但注意n取正整数这一条件.
解答:解:设{an}的公差为d,由题意得
a1+a3+a5=a1+a1+2d+a1+4d=105,即a1+2d=35,①
a2+a4+a6=a1+d+a1+3d+a1+5d=99,即a1+3d=33,②
由①②联立得a1=39,d=-2,
∴Sn=39n+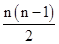 ×(-2)=-n2+40n=-(n-20)2+400,
×(-2)=-n2+40n=-(n-20)2+400,
故当n=20时,Sn达到最大值400.
故选B.
点评:求等差数列前n项和的最值问题可以转化为利用二次函数的性质求最值问题,但注意n取正整数这一条件.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源:2011年云南省高二上学期期中考试试题数学 题型:选择题
已知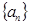 为等差数列,若
为等差数列,若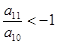 并且他的前n项和
并且他的前n项和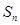 有最大值,那么当
有最大值,那么当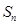 取得最小正值时,n=( )
取得最小正值时,n=( )
A.11 B 19 C 20 D 21
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com