练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求y=sinx+,x∈(0,]的最小值.

       

    解：设t=sinx,∵x∈(0,］,

    ∴t∈(0,1),则y=t+.

        设t1、t2∈(0,1］且t1＜t2,则y1-y2=t1+-t2-=(t1-t2)+=.

    ∵t1、t2∈(0,1］,∴t1t2-9＜0.

    ∵0＜t1＜t2≤1,∴t1t2＞0,t1-t2＜0.

    ∴＞0.∴y1＞y2.

    ∴y=t+在t∈(0,1)上是减函数.

    ∴ymin=10,当且仅当t=1即x=时,函数取到最小值.

    思维启示：利用基本不等式求最值的关键在于“一正、二定、三相等”,①一正:各项为正;②二定,要求积的最大值,则其和必须为定值,要求和的最值,其积必须为定值;③三相等:必须验证等号是否成立,否则容易导致错误,这一点同学们做题时最容易忽略.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知M(1+cos2x，1)，N(1，
    		3
    sin2x+a)    （x∈R，a∈R，a是常数），且y=
    OM
    •
    ON
    （O为坐标原点）．
    （1）求y关于x的函数关系式y=f（x）；
    （2）若x∈[0，
    π
    2
    ]    时，f（x）的最大值为4，求a的值；
    （3）在满足（2）的条件下，说明f（x）的图象可由y=sinx的图象如何变化而得到？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知
    a
    ，
    b
    是两个向量，且
    a
    =（1，
    		3
    cosx），
    b
    =（cos2x，sinx），x∈R，定义：y=
    a
    •
    b
    ．
    （1）求y关于x的函数解析式y=f（x）及其单调递增区间；?
    （2）若x∈[0，
    π
    2
    ]，求函数y=f（x）的最大值、最小值及其相应的x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知
    a
    =（y-m，sinx），
    b
    =（sinx-2m，1），且
    a
    ∥
    b
    ．
    （1）求y关于x的函数关系式y=f（x）；
    （2）求函数y=f（x）的最小值g（m）；
    （3）若g（m）＞-2，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2010年高三数学综合检测试卷2（必修4）（解析版） 题型：解答题

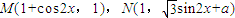    已知（x∈R，a∈R，a是常数），且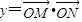（O为坐标原点）．
    （1）求y关于x的函数关系式y=f（x）；
    （2）若时，f（x）的最大值为4，求a的值；
    （3）在满足（2）的条件下，说明f（x）的图象可由y=sinx的图象如何变化而得到？

    查看答案和解析>>

    同步练习册答案