
| A�� | $\sqrt{5}$-1 | B�� | $\frac{3+\sqrt{5}}{2}$ | C�� | $\frac{\sqrt{5}+1}{2}$ | D�� | $\sqrt{3}$+1 |
���� ������ɵö��������˵����꼰�������꣬������εı߳������õȻ����ɵ�$\frac{1}{2}$•2b•2c=$\frac{1}{2}$a•4$\sqrt{{b}^{2}+{c}^{2}}$������a��b��c�Ĺ�ϵ�������ʹ�ʽ�����㼴�ɵõ�����ֵ��
���  �⣺������ɵ�A1��-a��0����A2��a��0����B1��0��b����B2��0��-b����
�⣺������ɵ�A1��-a��0����A2��a��0����B1��0��b����B2��0��-b����
F1��-c��0����F2��c��0����
��a2+b2=c2������F1B1F2B2�ı߳�Ϊ$\sqrt{{b}^{2}+{c}^{2}}$��
����A1A2Ϊֱ����Բ����������F1B1F2B2���е�ֱ�ΪA��B��C��D��
�������ȣ��ɵ�$\frac{1}{2}$•2b•2c=$\frac{1}{2}$a•4$\sqrt{{b}^{2}+{c}^{2}}$��
��Ϊb2c2=a2��b2+c2����
����c4+a4-3a2c2=0��
��e=$\frac{c}{a}$���ɵ�e4-3e2+1=0��
���e2=$\frac{3��\sqrt{5}}{2}$��
�ɵ�e=$\frac{1+\sqrt{5}}{2}$����e=$\frac{\sqrt{5}-1}{2}$����ȥ����
��ѡ��A��
���� ���⿼��˫���ߵ������ʵ���ע������Բ���еȻ��������黯�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���ͼ��ʾ���ھ���ABCD�У�AB=4��AD=2��E��CD���е㣬����ADE��AE����D1AEλ�ã�ʹƽ��D1AE��ƽ��ABCE���õ���ͼ��ʾ������D1-ABCE��
���ͼ��ʾ���ھ���ABCD�У�AB=4��AD=2��E��CD���е㣬����ADE��AE����D1AEλ�ã�ʹƽ��D1AE��ƽ��ABCE���õ���ͼ��ʾ������D1-ABCE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
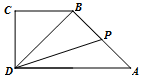 ��ͼ����ֱ������ABCD�У�AD��BC����ADC=90�㣬AD=2��BC=CD=1��P��AB���е㣬��$\overrightarrow{DP}•\overrightarrow{AB}$=-1��
��ͼ����ֱ������ABCD�У�AD��BC����ADC=90�㣬AD=2��BC=CD=1��P��AB���е㣬��$\overrightarrow{DP}•\overrightarrow{AB}$=-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
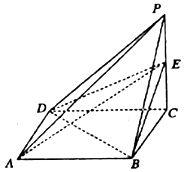 ��ͼ����֪����P-ABCD�DZ߳�Ϊ1�������Σ�PB=PD=$\sqrt{5}$��PC=2��E�Dz���PC�ϵĶ��㣮
��ͼ����֪����P-ABCD�DZ߳�Ϊ1�������Σ�PB=PD=$\sqrt{5}$��PC=2��E�Dz���PC�ϵĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{y}^{2}}{2}-\frac{{x}^{2}}{3}$=1 | B�� | y2-$\frac{{x}^{2}}{4}$=1 | C�� | $\frac{{y}^{2}}{4}$-x2=1 | D�� | $\frac{{y}^{2}}{3}-\frac{{x}^{2}}{2}$=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com