Question

已知数列{a_n}满足a₁=a(a≠0且a≠1)，其前n项的和S_n=(1-a_n).

（1）求证：{a_n}是等比数列.

（2）若a=,记b_n=a_nlg|a_n|(n∈N^*),问是否存在正整数m，使得对于任意正整数n,都有b_n≥b_m？若存在，求出m的值;若不存在，说明理由.

Answer 1

解：(1)令n=1，得a₁=a,1分当n≥2时，S_n=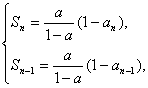

两式相减，结合a_n=S_n-S_n-1得=a_n-1.

∵a≠0,a≠1,a_n≠0,∴=a.

∴数列{a_n}是首项和公比均为a的等比数列.

(2)由（1）知a_n=aⁿ，当a=时，b_n=aⁿlg|aⁿ|=()ⁿnlg.

n为偶数时,b_n＜0,n为奇数时，b_n＞0.

∴设n为偶数，b_2n+2-b_n=()²ⁿ⁺²·(2n+2)lg-()²ⁿ·2n·lg=2·()ⁿlg·().

若b_2n+2＞b_2n,则7-2n＜0,2n＞7,b₈＜b₁₀＜b₁₂＜…，

若b_2n+2＜b_2n,则7-2n＞0,2n＜7,b₈＜b₆＜b₄＜b₂.

∴存在正整数m=8满足题设条件.