
已知递增等比数列 的第三项、第五项、第七项的积为512,且这三项分别减去1,3,9后成等差数列.
的第三项、第五项、第七项的积为512,且这三项分别减去1,3,9后成等差数列.
(1)求 的首项和公比;
的首项和公比;
(2)设 ,求
,求 .
.
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源:2011-2012学年上海市徐汇区高三4月学习能力诊断理科数学试卷(解析版) 题型:解答题
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
如果存在常数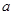 使得数列
使得数列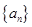 满足:若
满足:若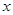 是数列
是数列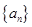 中的一项,则
中的一项,则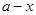 也是数列
也是数列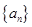 中的一项,称数列
中的一项,称数列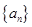 为“兑换数列”,常数
为“兑换数列”,常数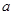 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列: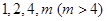 是“兑换系数”为
是“兑换系数”为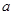 的“兑换数列”,求
的“兑换数列”,求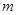 和
和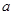 的值;
的值;
(2)已知有穷等差数列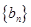 的项数是
的项数是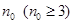 ,所有项之和是
,所有项之和是 ,求证:数列
,求证:数列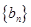 是“兑换数列”,并用
是“兑换数列”,并用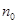 和
和 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列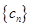 ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com