练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中，有一内角为60°,它的对边长为7，面积为103，则另两边长分别为________.

    思路分析：由S＝bcsinA=103,即bc×=103.

    得bc=40.                                                                                    ①

    又由余弦定理a2=b2+c2－2bccosA,即49＝b2+c2－bc,

    ∴b2+c2=89.

    由(b+c)2=b2+c2+2bc=89+2×40=169,得b+c=13.                        ②

    由①②,得解得或即另两边长分别为5、8.

    答案：5、8


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出下列命题：①sinα+cosα=
    1
    5
    ，则α在第一或四象限；②函数y=sinx+cosx，x=
    π
    4
    是它的一条对称轴，(
    3π
    4
    ，0)    是它的一个对称中心；③函数y=sin(2x-
    π
    3
    )    在[0，
    π
    2
    ]    内是单调增函数；④把y=2tan(2x+
    π
    3
    )    的图象向右平移
    π
    3
    个单位可得到y=2tan2x的图象；⑤在△ABC中，cos2A＞cos2B是A＜B的充要条件．
    其中逆否命题为真命题的有（　　）
    A、①②⑤B、②⑤
    C、②③④D、①③⑤

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，下列命题中正确的有：
    ③⑤
    ③⑤

    ①
    AB
    -
    AC
    =
    BC
    ；                
    ②若
    AC
    •
    AB
    ＞0    ，则△ABC为锐角三角形；
    ③O是△ABC所在平面内一定点，动点P满足
    OP
    =
    0A
    +λ(
    AB
    +
    AC
    )    ，λ∈[0，+∞），则动点P一定过△ABC的重心；
    ④O是△ABC内一定点，且
    OA
    +
    OC
    +2
    OB
    =
    0
    ，则
    S△AOC
    S△ABC
    =
    1
    3
    ；
    ⑤若（
    AB
    丨
    AB
    丨
    +
    AC
    丨
    AC
    丨
    ）•
    BC
    =0，且
    AB
    丨
    AB
    丨
    •
    AC
    丨
    AC
    丨
    =
    1
    2
    ，则△ABC为等边三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

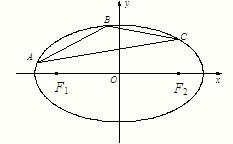    （2010•朝阳区二模）已知椭圆M：
    x2
    a2
    +
    y2
    b2
    =1 (a＞b＞0)    的左右焦点分别为F1（-2，0），F2（2，0）．在椭圆M中有一内接三角形ABC，其顶点C的坐标(
    		3
    ，1)    ，AB所在直线的斜率为
    		3
    3
    ．
    （Ⅰ）求椭圆M的方程；
    （Ⅱ）当△ABC的面积最大时，求直线AB的方程．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年福建省福州市高三上学期期末质量检测理科数学试卷（解析版） 题型：填空题

    给出下列命题：

    ①“x＝一1”是“x2一5x一6＝0”的必要不充分条件；

    ②在△ABC中，已知则;

    ③在边长为1的正方形ABCD内随机取一点M，MA＜1的概率为于

    ④若命题p是：:对任意的，都有sinx≤1,则为：存在,使得sinx > 1.

    其中所有真命题的序号是＿＿＿＿

     

    查看答案和解析>>

    科目：高中数学 来源：2010年北京市朝阳区高考数学二模试卷（文科）（解析版） 题型：解答题

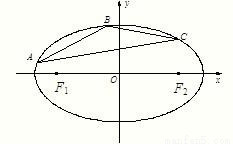
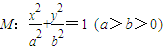    已知椭圆的左右焦点分别为F1（-2，0），F2（2，0）．在椭圆M中有一内接三角形ABC，其顶点C的坐标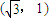，AB所在直线的斜率为．
    （Ⅰ）求椭圆M的方程；
    （Ⅱ）当△ABC的面积最大时，求直线AB的方程．

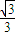    查看答案和解析>>

    同步练习册答案