
分析 (I)确定第7、8、9三题做对的概率,第10题做对的概率,运用题意得出P=${C}_{3}^{2}$($\frac{1}{2}$)2(1-$\frac{1}{2}$)(1$-\frac{1}{3}$)+${C}_{3}^{1}$×$\frac{1}{2}×$(1-$\frac{1}{2}$)2×$\frac{1}{3}$=$\frac{3}{8}$.
(II)确定概率分布需要的概率,求解E(X),利用互斥事件的概率问题求解.
解答 解:(Ⅰ) 第7、8、9三题均有两个选项能排除,
因此,第7、8、9三题做对的概率均为$\frac{1}{2}$,第10题只有一个选项能排除,
因此,第10题做对的概率为$\frac{1}{3}$.
所以,该同学选择题得40(分)的概率P为:
P=${C}_{3}^{2}$($\frac{1}{2}$)2(1-$\frac{1}{2}$)(1$-\frac{1}{3}$)+${C}_{3}^{1}$×$\frac{1}{2}×$(1-$\frac{1}{2}$)2×$\frac{1}{3}$=$\frac{3}{8}$
(Ⅱ)设该同学7、8、9、10题中做对的题数为X,则随机变量X的分布列为
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{12}$ | $\frac{7}{24}$ | $\frac{3}{8}$ | $\frac{5}{24}$ | $\frac{1}{24}$ |
点评 本题考查离散型随机变量的分布列和数学期望,考查学生的运算能力,考查学生探究研究问题的能力,解题时要认真审题,理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 16 | C. | 18 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
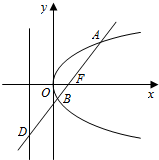 已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.
已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 π | B. | 2 π | C. | $\frac{4π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,16) | B. | [-1,16] | C. | (-1,$\frac{13}{4}$) | D. | [-1,$\frac{13}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
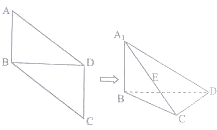 如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.
如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com