
设函数![]()
(1)写出函数![]() 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)![]() 时,函数
时,函数![]() 的最小值为2,求此时函数
的最小值为2,求此时函数![]() 的最大值,并指出
的最大值,并指出![]() 取何值时,函数
取何值时,函数![]() 取到最大值.
取到最大值.
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
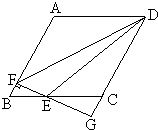 如图,在平行四边形ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于F,FE的延长线交DC的延长线于点G,设BE=x,△DEF的面积为S.
如图,在平行四边形ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于F,FE的延长线交DC的延长线于点G,设BE=x,△DEF的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:
 靠在墙角的梯子可看作线段AB(如图所示),AB的长是5米,这时梯子的下端B距墙根O的距离是3米,现将B沿OB的方向向右移动梯子的下端B,梯子的新位置是A′B′,直至A下落到墙根O为止.设AA′=x,BB′=y
靠在墙角的梯子可看作线段AB(如图所示),AB的长是5米,这时梯子的下端B距墙根O的距离是3米,现将B沿OB的方向向右移动梯子的下端B,梯子的新位置是A′B′,直至A下落到墙根O为止.设AA′=x,BB′=y查看答案和解析>>
科目:高中数学 来源:2013年山东省实验中学高考数学三模试卷(理科)(解析版) 题型:解答题
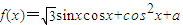 .
.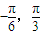 ]时,函数f(x)的最大值与最小值的和为
]时,函数f(x)的最大值与最小值的和为 ,求f(x)的解析式;
,求f(x)的解析式;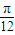 个单位,纵坐标不变横坐标变为原来的2倍,再向下平移
个单位,纵坐标不变横坐标变为原来的2倍,再向下平移 ,得到函数g(x),求g(x)图象与x轴的正半轴、直线
,得到函数g(x),求g(x)图象与x轴的正半轴、直线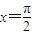 所围成图形的面积.
所围成图形的面积.查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省张家口市高考预测文科数学试卷(解析版) 题型:解答题
设函数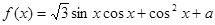
(I)写出函数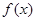 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(II)当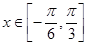 时,函数
时,函数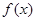 的最大值与最小值的和为
的最大值与最小值的和为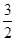 ,解不等式
,解不等式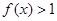 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com