练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求证：≥.

    思路解析：观察引导的特点，抽象出函数f（x）=,利用其单调性证明，还可利用分析法或综合法证明.

    证法一：（分析法）要证明≥,

    只需证（|a|+|b|）(1+|a+b|)≥|a+b|(1+|a|+|b|),

    只需证|a|+|b|+(|a|+|b|)·|a+b|≥|a+b|+(|a|+|b|)|a+b|,

    只需证|a|+|b|≥|a+b|,显然上式成立.

    所以原不等式成立.

    证法二：（利用函数的单调性）构造函数f(x)=(x≥0).

    ∵f(x)==1-,

    ∴函数f(x)在［0,+∞)上随x增大而增大，f(x)是增函数.

    ∵f(|a|+|b|)=,f(a+b)= ,|a|+|b|≥|a+b|,

    ∴f(|a|+|b|)≥f(|a+b|).∴≥.

    证法三:∵|a+b|≤|a|+|b|,|a+b|=0,显然成立.|a+b|≠0时，

    则=≤=.

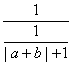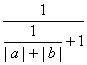    深化升华 

        由上面的证明还可得到以下结论：

    (1)≥;

    (2)若|a|≥|b|,则≤.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）的定义域为（0，+∞），对定义域内的任意x，y都有f（xy）=f（x）+f（y）-3
    （1）求f（1）的值；
    （2）求证：f(x)+f(
    1x
    )=6(x＞0)    ；
    （3）若x＞1时，f（x）＜3，判断f（x）在其定义域上的单调性，并证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在某两个正数x，y之间，若插入一个正数a，使x，a，y成等比数列；若插入两个正数b，c，使x，b，c，y成等差数列，求证：（a+1）2≤（b+1）（c+1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知cosθ=
    cosα-cosβ
    1-cosαcosβ
    ，求证：tan2
    θ
    2
    =tan2
    α
    2
    cot2
    β
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知：α，β为锐角，且3sin2α+2sin2β=1，3sin2α-2sin2β=0．求证：α+2β=
    π2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A、B、C同时满足sinA+sinB+sinC=0，cosA+cosB+cosC=0，求证：cos2A+cos2B+cos2C为定值．

    查看答案和解析>>

    同步练习册答案