解:(1)∵
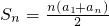
,∴2S
n=n(a
1+a
n)①
当n≥2时,2S
n-1=(n-1)(a
1+a
n-1)②
①-②得:2a
n=a
1+na
n-(n-1)a
n-1,即a
1+(n-2)a
n=(n-1)a
n-1③
进而a
1+(n-1)a
n+1=na
n④
③-④得2(n-1)a
n=(n-1)a
n-1+(n-1)a
n+1,由于n≥2,∴a
n+1-a
n=a
n-a
n-1所以数列{a
n}是等差数列.(4分)
(2)由(1)知数列{a
n}是等差数列,且a
1=1,a
2=2,所以a
n=n
∵

⑤
∴当n=1时,

,当n≥2时,

⑥
由⑤-⑥得:

,∴

,而

也符合,
故a
n=n,

(7分)
(3)

,∴T
n=1•3+2•3
2+…+n•3
n⑦3T
n=1•3
2+2•3
3+…+n•3
n+1⑧
⑦-⑧并化简得:

(10分)
所以


(2n
2+3n-2)•2
n-1=(2n-1)[3
n-(n+2)2
n-1]+1
因为3
n=(2+1)
n=2
n+C
n12
n-1+…≥2
n+n•2
n-1=(n+2)2
n-1所以3
n≥(n+2)2
n-1对于n∈N
*成立,
∴3
n-(n+2)2
n-1≥0,又由于2n-1>.0
所以

(2n
2+3n-2)•2
n-1=(2n-1)[3
n-(n+2)2
n-1]+1>0
所以

(2n
2+3n-2)•2
n-1(13分)
分析:(1)根据题目条件可得2S
n=n(a
1+a
n),则当n≥2时,2S
n-1=(n-1)(a
1+a
n-1)两式作差可得a
1+(n-2)a
n=(n-1)a
n-1,进而a
1+(n-1)a
n+1=na
n,两式作差可得a
n+1-a
n=a
n-a
n-1,根据等差数列数列的定义可得结论;
(2)根据等差数列的定义可求出其通项公式,利用递推关系可求出数列{b
n}的通项公式;
(3)利用错位相消法求出数列
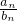
前n项和为T
n,然后利用作差可比较

与(2n
2+3n-2)•2
n-1的大小.
点评:本题主要考查了数列的递推关系,以及错位相消法的运用,同时考查了利用作差比较法比较大小,属于中档题.

 ;数列{bn}满足
;数列{bn}满足
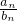 前n项和为Tn,试比较
前n项和为Tn,试比较 与(2n2+3n-2)•2n-1的大小.
与(2n2+3n-2)•2n-1的大小.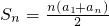 ,∴2Sn=n(a1+an)①
,∴2Sn=n(a1+an)① ⑤
⑤ ,当n≥2时,
,当n≥2时, ⑥
⑥ ,∴
,∴ ,而
,而 也符合,
也符合, (7分)
(7分) ,∴Tn=1•3+2•32+…+n•3n⑦3Tn=1•32+2•33+…+n•3n+1⑧
,∴Tn=1•3+2•32+…+n•3n⑦3Tn=1•32+2•33+…+n•3n+1⑧ (10分)
(10分)
 (2n2+3n-2)•2n-1=(2n-1)[3n-(n+2)2n-1]+1
(2n2+3n-2)•2n-1=(2n-1)[3n-(n+2)2n-1]+1 (2n2+3n-2)•2n-1=(2n-1)[3n-(n+2)2n-1]+1>0
(2n2+3n-2)•2n-1=(2n-1)[3n-(n+2)2n-1]+1>0 (2n2+3n-2)•2n-1(13分)
(2n2+3n-2)•2n-1(13分)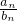 前n项和为Tn,然后利用作差可比较
前n项和为Tn,然后利用作差可比较 与(2n2+3n-2)•2n-1的大小.
与(2n2+3n-2)•2n-1的大小.

 名校课堂系列答案
名校课堂系列答案