练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数   求函数的定义域、值域

    解：由得 

    ∵xÎR,  ∴△0,  即 ,  ∴,  又∵，∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    ax2+1
    bx+c
    ，(a，b，c∈Z)    是奇函数，f（-1）=-2，f（2）＜3．
    （1）求函数f（x）解析式；
    （2）若g（x）=x•f（x），?（x）=g[g（x）]-λg（x），试问：是否存在实数λ，使∅（x）在（-∞，-1）内是单调递减，在（-1，0）内是单调递增的，若存在，求λ值；若不存在，说明理由．
    （3）附加题：若m(x)=f(x)-
    5
    x
    ，研究函数m（x），写出m（x）性质，并画出图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=mx2-x+lnx．
    （1）当m=-1时，求f（x）的最大值；
    （2）若在函数f（x）的定义域内存在区间D，使得该函数在区间D上为减函数，求m的取值范围；
    （3）当m＞0时，若曲线C：y=f（x）在点x=1处的切线l与C有且只有一个公共点，求m的值．

    查看答案和解析>>

    科目：高中数学 来源：广东省执信中学2011届高三2月月考数学理科试题 题型：047

    已知函数

    (Ⅰ)求函数的定义域，并证明在定义域上是奇函数；

    (Ⅱ)若恒成立，求实数m的取值范围；

    (Ⅲ)当时，试比较与2n＋2n2的大小关系．

    查看答案和解析>>

    科目：高中数学 来源：2015届浙江省绍兴市高一上学期阶段性考试数学试卷（解析版） 题型：解答题

    已知函数有如下性质：如果常数，那么该函数在上是减函数，在 上是增函数．

    （1）如果函数在上是减函数，在上是增函数，求的值；

    （2）证明：函数（常数）在上是减函数；

    （3）设常数，求函数的最小值和最大值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014届山东省济宁市高一下学期期中数学试卷（解析版） 题型：解答题

    已知函数。

    （1）求函数的最小正周期和最大值；

    （2）求函数的增区间；

    （3）函数的图象可以由函数的图象经过怎样的变换得到？

    【解析】本试题考查了三角函数的图像与性质的运用。第一问中，利用可知函数的周期为，最大值为。

    第二问中，函数的单调区间与函数的单调区间相同。故当，解得x的范围即为所求的区间。

    第三问中，利用图像将的图象先向右平移个单位长度，再把横坐标缩短为原来的 （纵坐标不变），然后把纵坐标伸长为原来的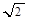倍（横坐标不变），再向上平移1个单位即可。

    解：（1）函数的最小正周期为，最大值为。

    （2）函数的单调区间与函数的单调区间相同。

     即

    所求的增区间为，

    即

    所求的减区间为，。

    （3）将的图象先向右平移个单位长度，再把横坐标缩短为原来的 （纵坐标不变），然后把纵坐标伸长为原来的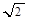倍（横坐标不变），再向上平移1个单位即可。

     

    查看答案和解析>>

    同步练习册答案