
已知p:∀x∈R,2x>m(x2+1),q:∃x0∈R,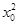 +2x0-m-1=0,且p∧q为真,求实数m的取值范围.
+2x0-m-1=0,且p∧q为真,求实数m的取值范围.
-2≤m<-1.
【解析】
试题分析:2x>m(x2+1) 可化为mx2-2x+m<0.
所以若p:∀x∈R, 2x>m(x2+1)为真,
则mx2-2x+m<0对任意的x∈R恒成立.
由此可得m的取值范围.
若q:∃x0∈R,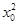 +2x0-m-1=0为真,
+2x0-m-1=0为真,
则方程x2+2x-m-1=0有实根,由此可得m的取值范围.
p∧q为真,则p、q 均为真命题,取m的公共部分便得m的取值范围.
试题解析:2x>m(x2+1) 可化为mx2-2x+m<0.
若p:∀x∈R, 2x>m(x2+1)为真,
则mx2-2x+m<0对任意的x∈R恒成立.
当m=0时,不等式可化为-2x<0,显然不恒成立;
当m≠0时,有m<0,Δ= 4-4m2<0,∴m<-1.
若q:∃x0∈R,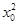 +2x0-m-1=0为真,
+2x0-m-1=0为真,
则方程x2+2x-m-1=0有实根,
∴Δ=4+4(m+1)≥0,∴m≥-2.
又p∧q为真,故p、q 均为真命题.
∴m<-1且m≥-2,∴-2≤m<-1.
考点:1、全称命题与特称命题;2、逻辑连结词.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年河北省高三12月月考理科数学试卷(解析版) 题型:选择题
已知命题p:∀x∈(0, ),3x>2x,命题q:∃x∈(
),3x>2x,命题q:∃x∈( ,0),
,0), ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )
A . p∧q B .(¬p)∧q C.(¬p)∧(¬q) D.p∧(¬q)
查看答案和解析>>
科目:高中数学 来源:2014届四川省成都高新区高三10月统一检测理科数学试卷(解析版) 题型:选择题
已知命题p:
∀x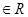 ,
,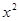 >0,则(
)
>0,则(
)
A.非p:∃x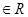 ,
,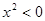 B.非p:∀x
B.非p:∀x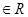 ,
,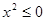
C.非p:∃x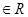 ,
,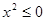 D.非p:∀x
D.非p:∀x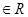 ,
,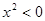
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学选修2-1 1.4全称量词与存在量词练习卷(解析版) 题型:选择题
已知命题p:∀x∈R,sin x≤1,则( )
A.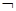 p:∃x0∈R,sin
x0≥1
p:∃x0∈R,sin
x0≥1
B.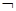 p:∀x∈R,sin x≥1
p:∀x∈R,sin x≥1
C.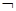 p:∃x0∈R,sin
x0>1
p:∃x0∈R,sin
x0>1
D.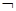 p:∀x∈R,sin x>1
p:∀x∈R,sin x>1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com