练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若a＞b＞1，m＝a＋lgb，n＝b＋lga，则

    [　　]
    A．

    m＞n

    B．

    m＝n

    C．

    m＜n

    D．

    以上都有可能

    答案：A
    解析：

    　　分析：根据两个式子的结构特征，可联想构造函数f(x)＝x－lgx，利用其单调性比较大小．由于用定义判断这个函数的单调性比较困难，因此我们考虑借助函数y＝x，y＝lgx的图象判断其单调性．

    　　解：构造函数f(x)＝x－lgx，在同一平面直角坐标系中分别画出函数y＝x，y＝lgx的图象，如图所示．

    　　观察图象不难发现，当x＞1时，随着x的增大，x－lgx的值也逐渐增大，所以函数f(x)＝x－lgx在区间(1，＋∞)上是增函数．

    　　因为a＞b＞1，所以a－lga＞b－lgb，所以a＋lgb＞b＋lga，即m＞n．故选A．

    　　点评：比较大小是函数单调性的一个重要应用．本题通过构造函数，利用其单调性解决问题．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2002年全国各省市高考模拟试题汇编 题型：044

    已知f(x)是定义在[－1，1]上的奇函数，且f(1)＝1，若a，b∈[－1，1]，a＋b≠0有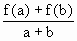＞0，

    (Ⅰ)判断函数f(x)在[－1，1]上是增函数，还是减函数，并证明你的结论；

    (Ⅱ)解不等式；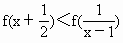

    (Ⅲ)若f(x)≤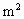－2am＋1，对所有x∈[－1，1]，a∈[－1，1]恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知f(x)是定义在[－1，1]上的奇函数，且f(1)＝1，若a，b∈[－1，1]，a＋b≠0有＞0恒成立．

    (Ⅰ)判断f(x)在[－1，1]上是增函数还是减函数，并证明你的结论；

    (Ⅱ)解不等式f(x＋)＜f()；

    (Ⅲ)若f(x)≤m2－2am＋1，对所有x∈[－1，1]，a∈[－1，1]恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知f(x)是定义在[－1，1]上的奇函数，且f(1)＝1，若a，b∈[－1，1]，a＋b≠0有＞0

    (1)判断函数f(x)在[－1，1]上是增函数，还是减函数，并证明你的结论；

    (2)解不等式f(x＋)＜f()；

    (3)若f(x)≤m2－2am＋1，对所有x∈[－1，1]a∈[－1，1]恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    已知f（x）是定义在[－1，1]上的奇函数，且f（1）＝1，若a，b∈[－1，1]，a＋b≠0有恒成立．

    　　（Ⅰ）判断f（x）在[－1，1]上是增函数还是减函数，并证明你的结论；

    　　（Ⅱ）解不等式；

    　　（Ⅲ）若f（x）≤－2am＋1，对所有x∈[－1，1]，a∈[－1，1]恒成立，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案