
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
| 2an |
| 2n+2 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| lim |
| n→∞ |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市虹口区高三第一学期期末教学质量监控测试卷数学 题型:解答题
(15分)已知 是数列
是数列 的前
的前 项和,
项和, (
( ,
, ),且
),且 .
.
(1)求 的值,并写出
的值,并写出 和
和 的关系式;
的关系式;
(2)求数列 的通项公式及
的通项公式及 的表达式;
的表达式;
(3)我们可以证明:若数列 有上界(即存在常数
有上界(即存在常数 ,使得
,使得 对一切
对一切 恒成立)且单调递增;或数列
恒成立)且单调递增;或数列 有下界(即存在常数
有下界(即存在常数 ,使得
,使得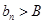 对一切
对一切 恒成立)且单调递减,则
恒成立)且单调递减,则 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: 存在.
存在.
查看答案和解析>>
科目:高中数学 来源: 题型:
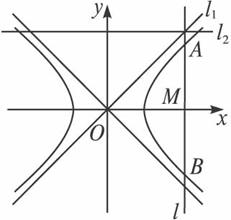
(1)求双曲线C的离心率;
(2)求双曲线C的方程.
(文)已知公差不为零的等差数列{an}的前n项和为Sn,Sn及通项an满足关系式:4Sn=an2+αan+β(α、β为常数,n∈N+),且a1=-1.
(1)求常数α、β的值;
(2)求数列{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com