解:(Ⅰ)∵c=﹣a
2,
∴f ' (x)=3ax
2+2bx﹣a
2,
∵x
1、x
2是方程3ax
2+2bx﹣a
2=0的两根,a>0,
∴x
1+x
2=﹣
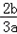
,x
1x
2=﹣

;
∵|x
1﹣x
2|=2,
∴
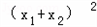
﹣4x1x2=4,即
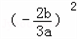
﹣4(﹣

)=4,
整理得b
2=3a
2(3﹣a),
∵b
2≥0,∴0<a≤3;
设h(a)=﹣3a
3+9a
2,
则h'(a)=﹣9a
2+18a;
由h'(a)>0,得0<a<2;由h'(a)<0,得a>2.
∴h(a)=﹣3a
3+9a
2在区间(0,2)上是增函数,在区间(2,3)上是减函数,
∴当a=2时,h(a)有极大值12,
∴h(a)在(0,3]上的最大值是12,
从而b的最大值是2
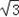
(Ⅱ)由g(x)=f '(x)+x,得f '(x)=g(x)﹣x,
∵x
1、x
2是方程f '(x)=0的两根,
∴f '(x)=g(x)﹣x=3a(x﹣x
1)(x﹣x
2),当x∈(0,x
1)时,由于x
1<x
2,
故(x﹣x
1)(x﹣x
2)>0,又a>0,
故g(x)﹣x=3a(x﹣x
1)(x﹣x
2)>0,即g(x)>x;
又x
1﹣g(x)=x
1﹣[x+f '(x)]=x
1﹣x﹣3a(x﹣x
1)(x﹣x
2)=(x
1﹣x)[1+3a(x﹣x
2)],
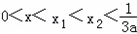
,
∴x
1﹣x>0,[1+3a(x﹣x
2)]=1+3ax﹣3ax
2>1﹣3ax
2>0,
∴g(x)<x
1;
综上所述:x<g(x)<x
1.

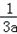 ,且x∈(0,x1),证明:x<g(x)<x1.
,且x∈(0,x1),证明:x<g(x)<x1.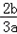 ,x1x2=﹣
,x1x2=﹣ ;
;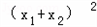 ﹣4x1x2=4,即
﹣4x1x2=4,即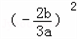 ﹣4(﹣
﹣4(﹣ )=4,
)=4,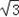
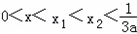 ,
,
