
分析 (Ⅰ)得分为45分,剩下4道必须再做对3道题,在其余的四道题中,有两道题答对的概率为$\frac{1}{2}$,有一道题答对的概率为$\frac{1}{3}$,还有一道答对的概率为$\frac{1}{4}$,由此能求出得分为45分的概率.
(Ⅱ)依题意,该考生得分的范围为{30,35,40,45,50},分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答 解:(Ⅰ)得分为45分,剩下4道必须再做对3道题,在其余的四道题中,
有两道题答对的概率为$\frac{1}{2}$,有一道题答对的概率为$\frac{1}{3}$,还有一道答对的概率为$\frac{1}{4}$,
所以得分为45分的概率为:
$P=\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{3}{4}+\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{1}{4}+\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{1}{4}+\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{1}{4}=\frac{7}{48}$.
(Ⅱ)依题意,该考生得分的范围为{30,35,40,45,50}.
得分为30分表示只做对了6道题,其余各题都做错,所以概率为:${P_1}=\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{3}{4}=\frac{6}{48}=\frac{1}{8}$;
同理可以求得得分为35分的概率为:${P_2}=C_2^1×\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{3}{4}+\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{3}{4}+\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{1}{4}=\frac{17}{48}$;
得分为40)的概率为:${P_3}=\frac{17}{48}$;
得分为45)的概率为:${P_4}=\frac{7}{48}$;
得分为50)的概率为:${P_5}=\frac{1}{48}$.
可知ξ的分布列为:
| ξ | 30 | 35 | 40 | 45 | 50 |
| P | $\frac{6}{48}$ | $\frac{17}{48}$ | $\frac{17}{48}$ | $\frac{7}{48}$ | $\frac{1}{48}$ |
点评 本题考查考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,考查数据处理能力、运算求解能力,考查化归与转化思想、函数与方思想,是中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 320 | B. | 446 | C. | 482 | D. | 248 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
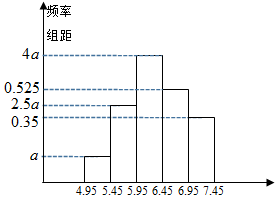 质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下:
质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②⑤ | B. | ①②③ | C. | ①④⑤ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com