练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    等差数列{an} 中，若a2+a3=4，a8+a9=36，则S10等于（ ）
    A．40
    B．80
    C．90
    D．100
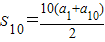
    【答案】分析：由等差数列的求和公式可知，，故需要求a1+a10，根据等差数列的性质可知a2+a9=a3+a8=a1+a10，结合已知可求
    解答：解：∵a2+a3=4，a8+a9=36，
    ∵a2+a3+a8+a9=40，
    由等差数列的性质可知，a2+a9=a3+a8=a1+a10=20
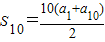
    由等差数列的求和公式可知，=5×20=100
    故选D
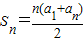
    点评：本题主要考查了等差数列性质（若m+n=p+q，则am+an=ap+aq）及等差数列的求和公式的应用
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知等差数列{an}中，a1=-4，且a1、a3、a2成等比数列，使{an}的前n项和Sn＜0时，n的最大值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等差数列﹛an﹜中，a3=5，a15=41，则公差d=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等差数列{an }中，an≠0，且 an-1-an2+an+1=0，前（2n-1）项和S2n-1=38，则n等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，设S1=10，S2=20，则S10的值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）在等差数列{an}中，d=2，a15=-10，求a1及Sn；
    （2）在等比数列{an}中，a3=
    3
    2
    ，S3=
    9
    2
    ，求a1及q．

    查看答案和解析>>

    同步练习册答案