
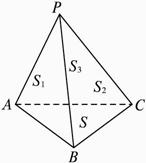
解:如图所示,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示平面PAB与平面PBC,平面PBC与平面PCA,平面PCA与平面PAB所成二面角的大小,猜想余弦定理类比推理到三维空间的表现形式应为?
S2=S12+S22+S32-2S1S2coSα-2S2S3coSβ-2S3S1coSγ.?
上式可叙述为四面体的一个面的面积的平方,等于其他各面面积平方的和,减去每两个面面积与这两个面夹角余弦乘积的两倍.?
关于三维余弦定理的证明问题我们可以类比平面中的三角形射影定理来证明三角形余弦定理的方法,给出较简捷的证法.?
先看由三角形射影定理证明其余弦定理的方法:在△ABC中,A、b、c分别表示角A、B、C的对边,则有?
A=bcoSC+ccoSB, ①?
b=ccoSA+AcoSC, ②?
c=AcoSB+bcoSA. ③?
①×A-②×b-③×c可得?
A2-b2-c2=-2bccoSA,?
∴A2=b2+c2-2bccoSA.?
下面给出三维余弦定理的证明,如图,记号![]() 表示面积为S1和S2的两个面所成的二面角大小,由例1的三维射影定理可知:?
表示面积为S1和S2的两个面所成的二面角大小,由例1的三维射影定理可知:?
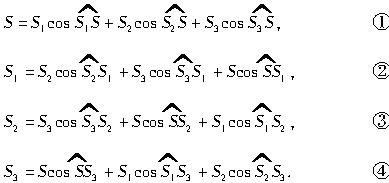 o
o
①×S-②×S1-③×S2-④×S3可得S2-S12-S22-S32?
![]()
=-2S1S2coSα-2S2S3coSβ-2S3S1coSγ,?
移项得欲证三维余弦定理.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
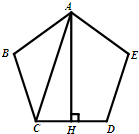 如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得AC=
如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得AC=| 8-8cos108° |
| 1 |
| cos72° |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建师大附中高三(上)期中数学试卷(理科)(解析版) 题型:选择题
 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得 ,据此可得cos72°的值所在区间为( )
,据此可得cos72°的值所在区间为( )
查看答案和解析>>
科目:高中数学 来源:2012年福建省厦门市高三3月质量检查数学试卷(理科)(解析版) 题型:选择题
 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得 ,据此可得cos72°的值所在区间为( )
,据此可得cos72°的值所在区间为( )
查看答案和解析>>
科目:高中数学 来源:2011年福建省高三质量检查数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com